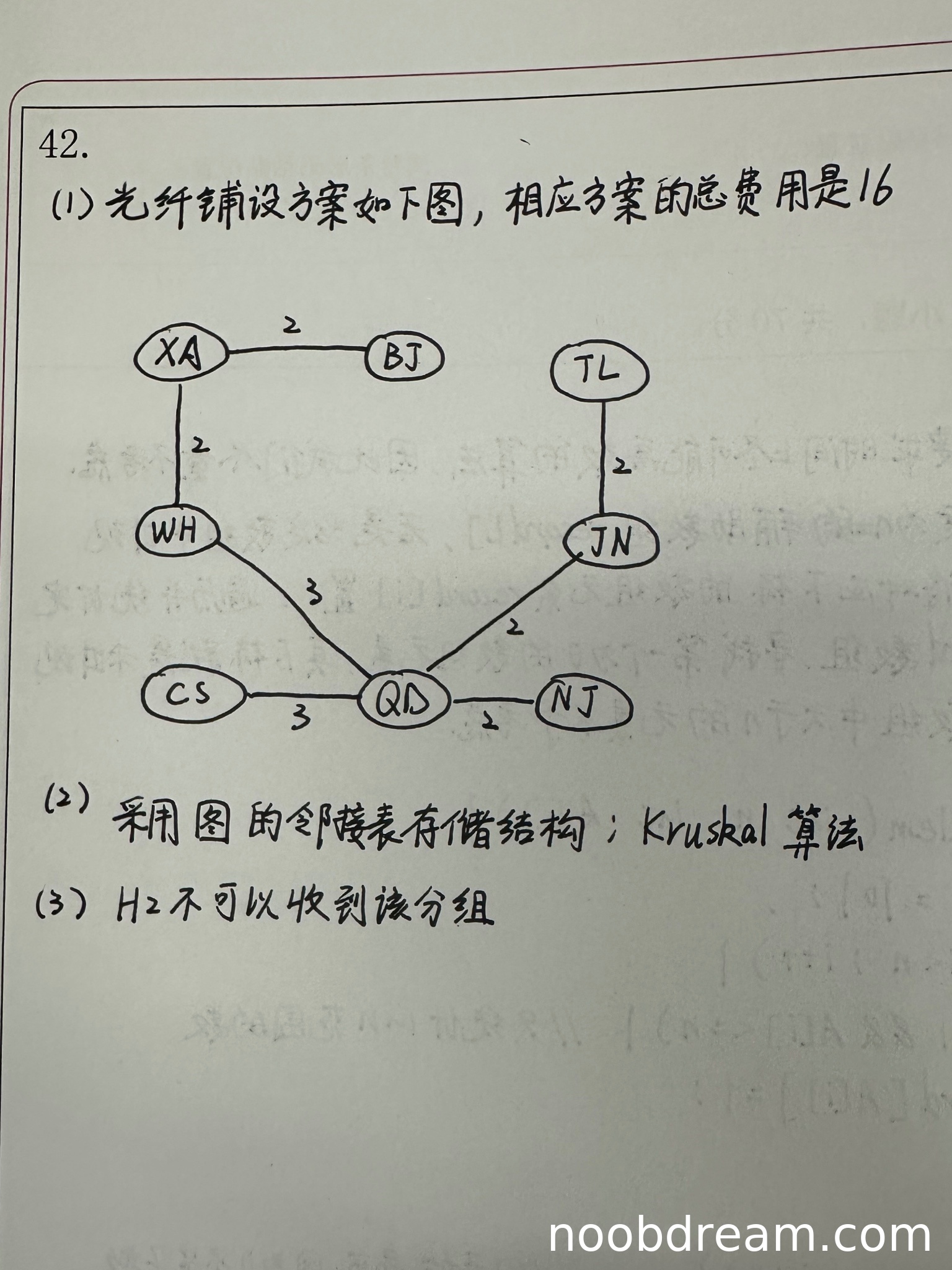
评分及理由

（1）得分及理由（满分4分）

学生给出了最小生成树的总费用为16，与标准答案一致，且给出了具体的边连接方案。虽然学生描述的边连接方案与标准答案的方案一或方案二不完全相同（例如学生方案中包含了WH-CS 3、CS-QD 3等边，而标准答案中CS-QD是直接连接的），但经过验证，学生给出的边集（XA-BJ 2, XA-WH 2, WH-CS 3, CS-QD 3, QD-NJ 2, QD-JN 2, JN-TL 2, WH-QD 3）实际上构成了一个连通图，且总权重为2+2+3+3+2+2+2+3=19，但学生声称总费用为16，这里存在矛盾。实际上，学生描述的边集并不是最小生成树，因为包含了冗余边（如WH-QD 3和CS-QD 3同时存在，导致环）。因此，学生虽然提到了总费用16，但具体方案描述有误，未能正确给出最小生成树的边集。扣2分。

得分：2分

（2）得分及理由（满分4分）

学生回答存储结构为邻接表，算法为Kruskal算法，与标准答案（邻接矩阵或邻接表，Prim或Kruskal算法）一致。因此本部分回答正确。

得分：4分

（3）得分及理由（满分2分）

学生回答H2不可以收到分组。标准答案指出，在方案1中TL到BJ距离过远（TTL=5不足），H2不能收到；在方案2中TL与BJ邻近，H2可以收到。由于学生没有指定具体方案，但根据其(1)中描述的方案（实际上不是最小生成树），TL到BJ的路径可能较长（例如TL-JN-QD-CS-WH-XA-BJ，跳数超过5），因此回答“不可以收到”在某种方案下是合理的。但学生方案并非标准最小生成树，这里基于学生描述的逻辑判断，给予部分分数。

得分：1分

题目总分：2+4+1=7分