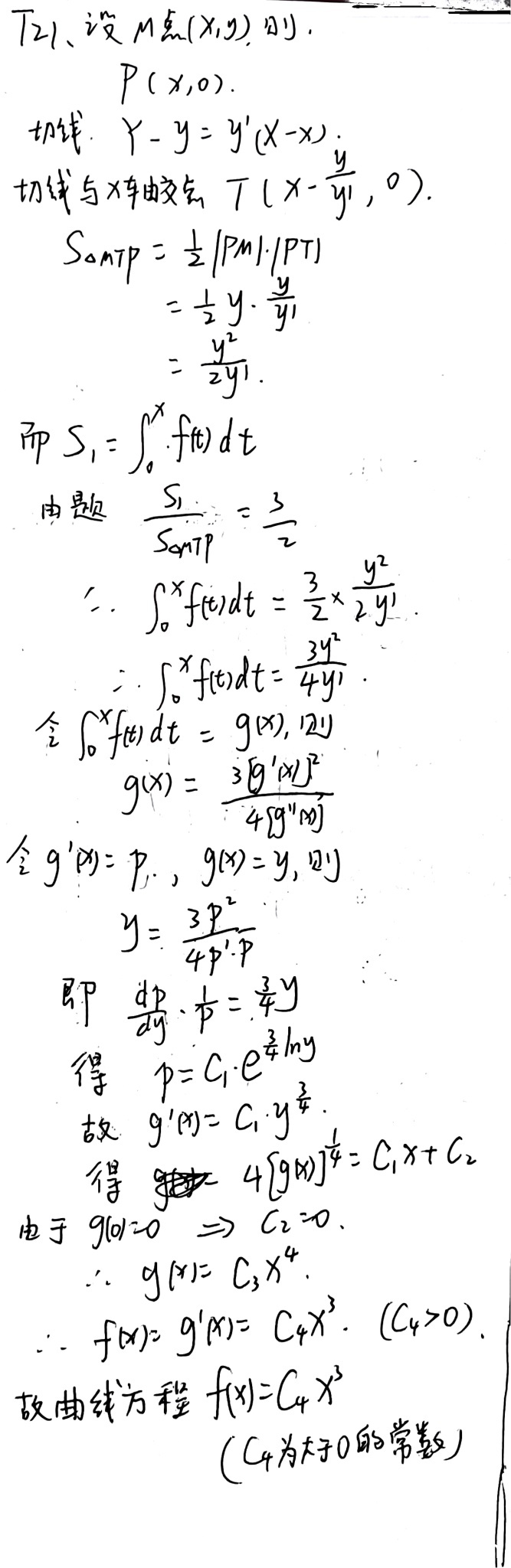
评分及理由

（1）得分及理由（满分10分）

学生正确设定了点M、P、T的坐标，并正确计算了三角形MTP的面积 \(S_{\triangle MTP} = \frac{y^2}{2y'}\) 以及由曲线、MP和x轴围成的面积 \(S_1 = \int_0^x f(t)dt\)。根据题目条件建立了面积比方程 \(\int_0^x f(t)dt = \frac{3y^2}{4y'}\)，这部分逻辑正确，得4分。

（2）得分及理由（满分10分）

学生在后续求解微分方程时出现了逻辑错误。标准答案通过对方程两边求导得到 \(3yy'' = 2(y')^2\)，而学生错误地引入了 \(g(x) = \int_0^x f(t)dt\) 并推导出 \(g(x) = \frac{3[g'(x)]^2}{4g''(x)}\)，这步转换存在错误。后续求解过程中，学生得到 \(p = C_1 y^{3/4}\) 而不是正确的 \(p = C_1 y^{2/3}\)，导致最终结果虽然形式类似但推导过程错误。这部分逻辑错误严重，扣6分，得4分。

（3）得分及理由（满分10分）

学生最终得到了 \(f(x) = C_4 x^3\) 的正确形式，且注意到常数 \(C_4 > 0\)，这与标准答案一致。虽然推导过程有误，但最终结果正确，考虑到题目要求"思路正确不扣分"但实际推导存在逻辑错误，根据评分原则对逻辑错误扣分，但最终结果正确给予部分分数，得6分。

题目总分：4+4+6=14分