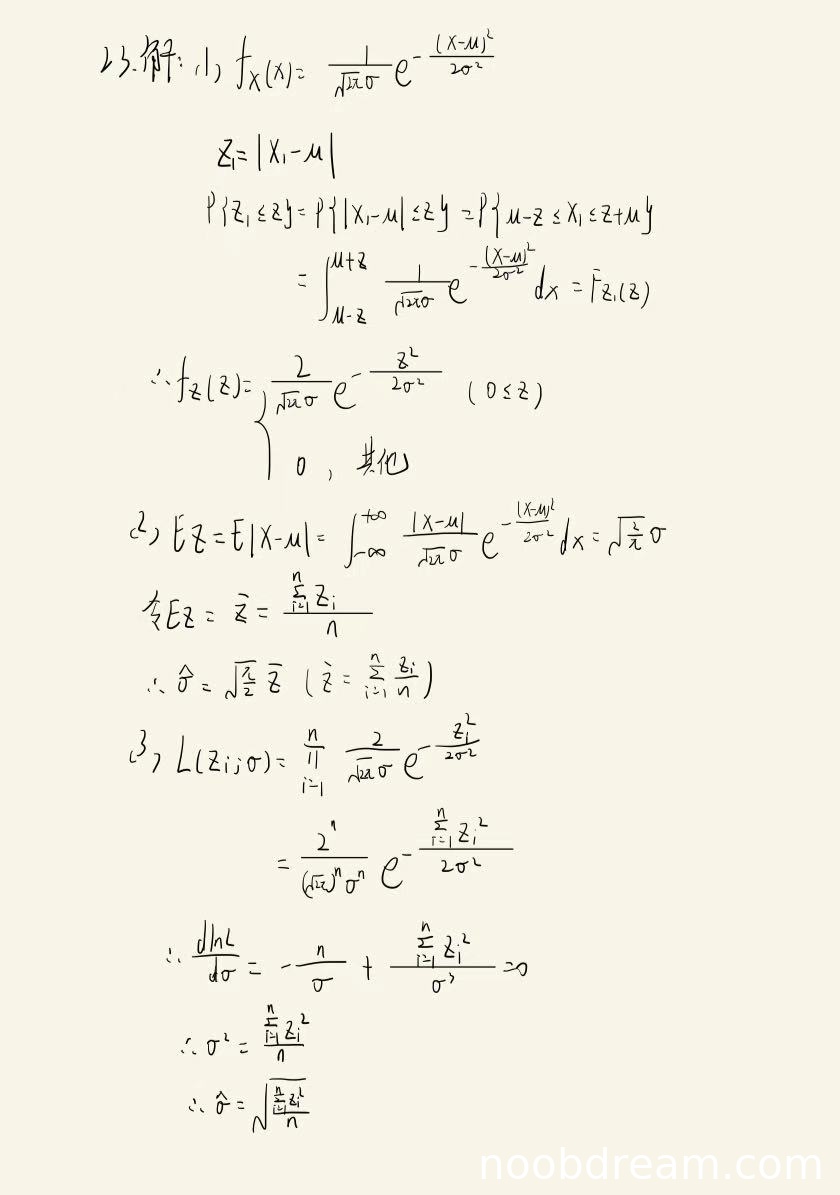
评分及理由

（1）得分及理由（满分4分）

学生正确推导了Z_i的概率密度函数。通过分布函数求导得到概率密度，过程完整，结果正确。虽然第一次识别结果中分布函数推导过程略显简略，但第二次识别结果补充了完整过程。因此给满分4分。

（2）得分及理由（满分3分）

学生正确计算了EZ = √(2/π)σ，并利用一阶矩得到了矩估计量。虽然学生写的是√(π/2)z̄，这与标准答案的(√(2π)/2)z̄在数值上是相等的（因为√(π/2) = √(2π)/2）。这是一个等价表达，思路和结果都正确。因此给满分3分。

（3）得分及理由（满分4分）

学生正确建立了似然函数，进行了对数变换，求导并解出了最大似然估计量。推导过程完整，结果与标准答案一致。因此给满分4分。

题目总分：4+3+4=11分