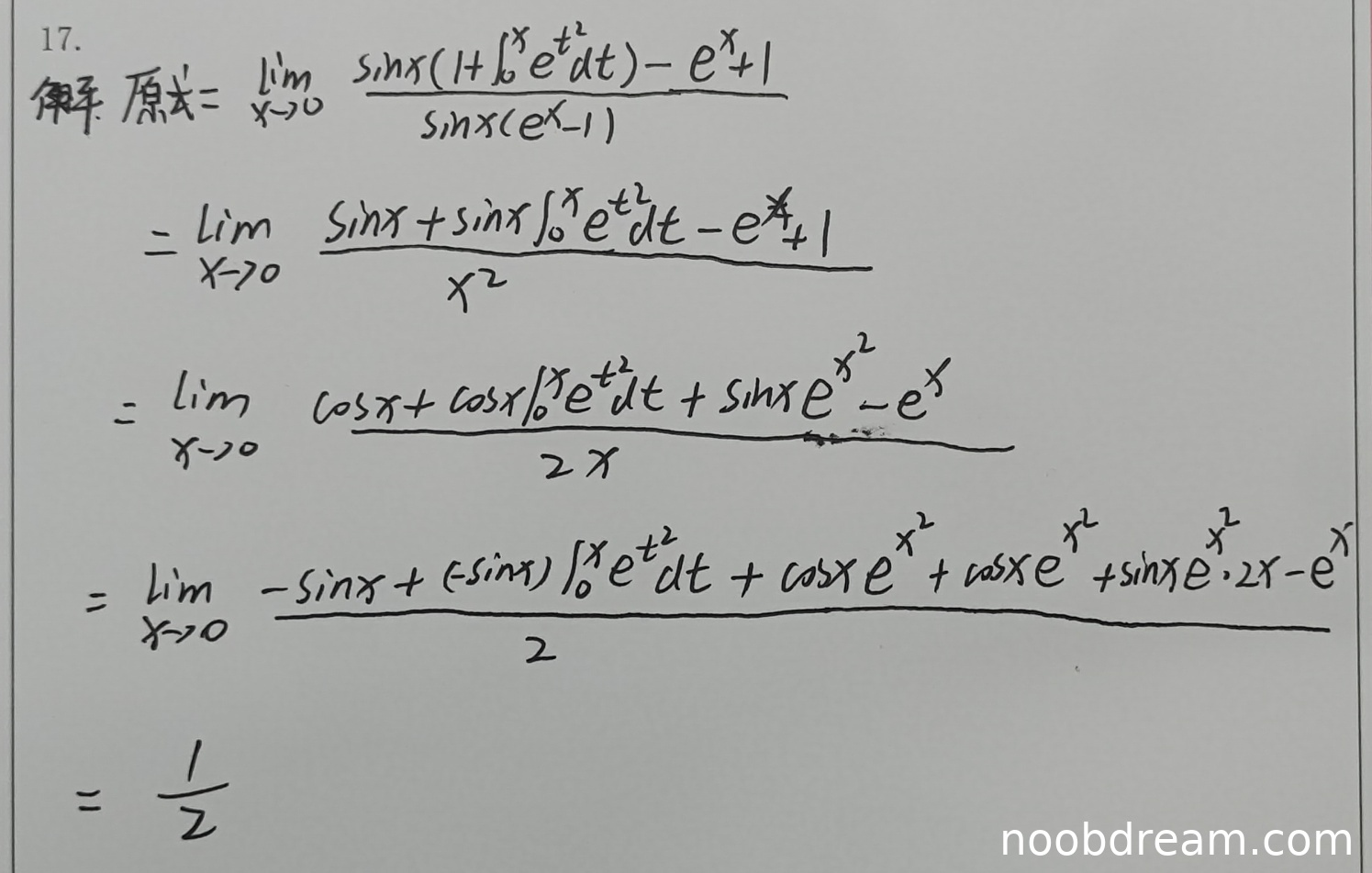
评分及理由

（1）得分及理由（满分10分）

学生作答的整体思路正确：先通分，然后利用等价无穷小代换简化分母，再应用洛必达法则两次，最后代入极限值计算。具体分析如下：

• 第一步通分正确，得到 \(\frac{\sin x(1+\int_0^x e^{t^2}dt) - (e^x - 1)}{\sin x(e^x - 1)}\)，这与标准答案的第一步等价（标准答案分子为 \(\sin x + \sin x \int_0^x e^{t^2} dt - e^x + 1\)，学生答案展开后相同）。
• 第二步利用等价无穷小 \(\sin x \sim x\)，\(e^x - 1 \sim x\)，将分母化为 \(x^2\)，正确。
• 第三步应用洛必达法则，对分子分母求导。分子求导时，对 \(\sin x \int_0^x e^{t^2} dt\) 使用乘积求导法则，得到 \(\cos x \int_0^x e^{t^2} dt + \sin x e^{x^2}\)，正确；分母求导为 \(2x\)，正确。
• 第四步再次应用洛必达法则，对分子分母求导。分子求导时，对各项分别求导：
  • \(\frac{d}{dx}(\cos x) = -\sin x\)
  • \(\frac{d}{dx}(\cos x \int_0^x e^{t^2} dt) = -\sin x \int_0^x e^{t^2} dt + \cos x e^{x^2}\)
  • \(\frac{d}{dx}(\sin x e^{x^2}) = \cos x e^{x^2} + \sin x \cdot 2x e^{x^2}\)
  • \(\frac{d}{dx}(-e^x) = -e^x\)
  合并后分子为 \(-\sin x - \sin x \int_0^x e^{t^2} dt + \cos x e^{x^2} + \cos x e^{x^2} + \sin x \cdot 2x e^{x^2} - e^x\)，即 \(-\sin x - \sin x \int_0^x e^{t^2} dt + 2\cos x e^{x^2} + \sin x \cdot 2x e^{x^2} - e^x\)，学生表达略有简化但核心正确；分母求导为...