文章
149
粉丝
195
获赞
0
访问
19.1k

2025年张宇终极预测8套卷(三) - 第17题回答
1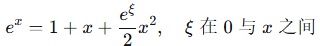
2: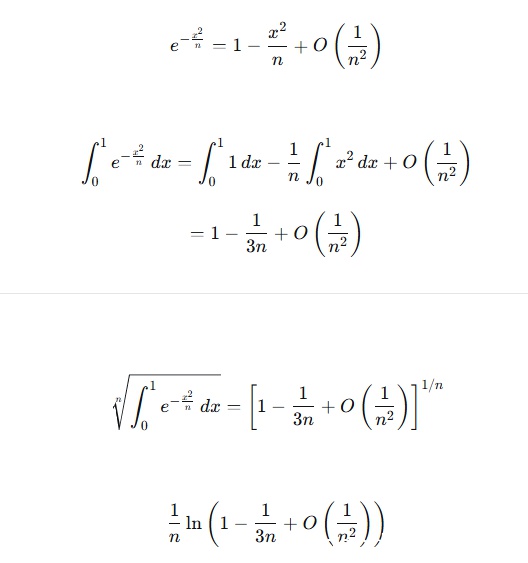
原极限=e^0=1
评分及理由
(1)得分及理由(满分5分)
学生答案:\(e^{x}=1+x+\frac{e^{\xi}}{2}x^{2}\),\(\xi\)在\(0\)与\(x\)之间
标准答案:\(\mathrm{e}^{x}=1 + x + \frac{\mathrm{e}^{\xi}}{2}x^{2}\),\(\xi\)介于\(0\),\(x\)之间
评分:5分
理由:学生答案与标准答案完全一致,正确写出了带拉格朗日余项的麦克劳林公式,余项形式正确,\(\xi\)的范围描述准确。
(2)得分及理由(满分5分)
学生答案:原极限=e^0=1
标准答案:通过麦克劳林展开和积分计算得到极限为1
评分:0分
理由:学生直接给出结果"原极限=e^0=1",但完全没有展示计算过程。题目要求计算极限\(\lim\limits_{n\to\infty}\sqrt[n]{\int_{0}^{1}\mathrm{e}^{-\frac{x^{2}}{n}}\mathrm{d}x}\),这是一个需要详细推导的过程。学生没有使用第(1)问的麦克劳林公式,也没有展示任何积分计算步骤,直接跳跃到最终答案,属于严重的逻辑缺失。虽然最终答案正确,但缺乏必要的推导过程,不能得分。
题目总分:5+0=5分


 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1



登录后发布评论
暂无评论,来抢沙发