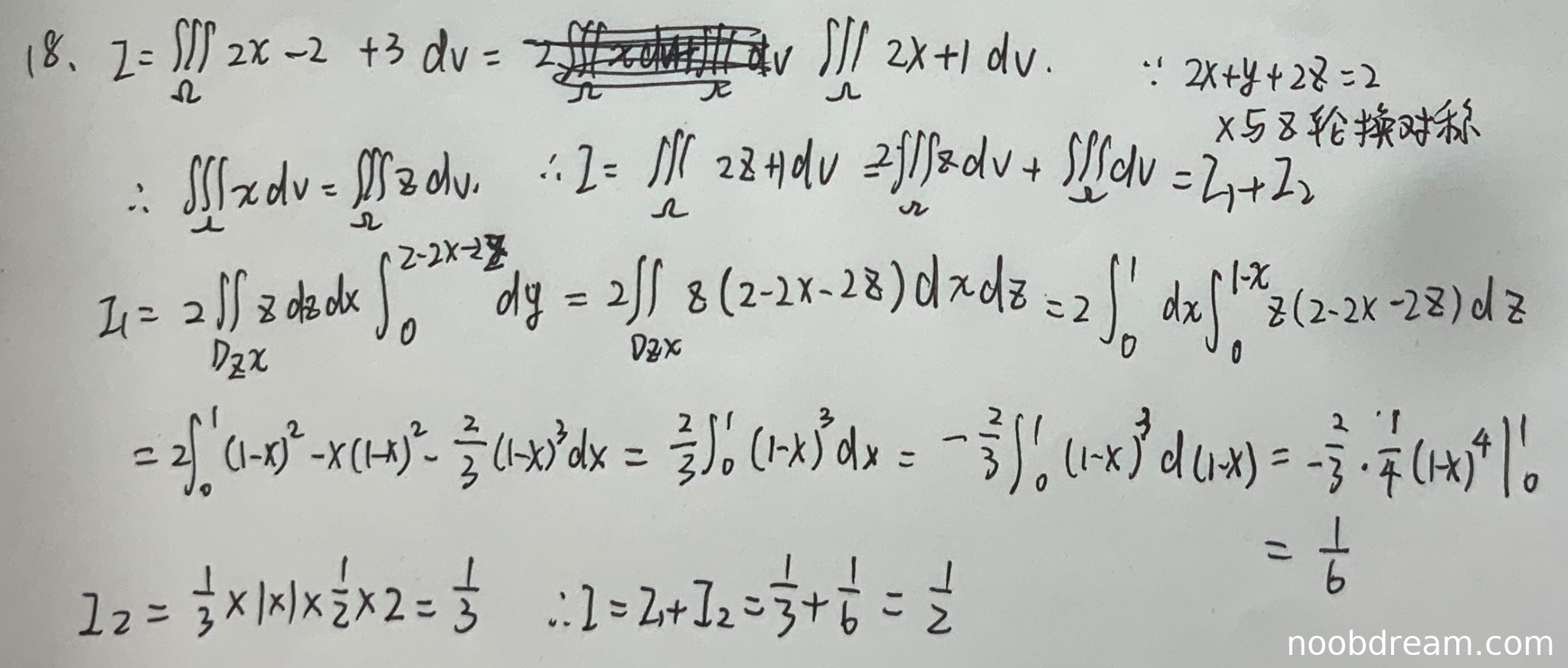
评分及理由

（1）高斯公式应用部分（满分2分）

学生正确应用了高斯公式将曲面积分转化为三重积分，得到 \(\iiint_{\Omega}(2x+1)dV\)，与标准答案一致。此处无逻辑错误，得2分。

（2）积分计算过程（满分6分）

学生采用轮换对称性 \(\iiint_{\Omega}xdV=\iiint_{\Omega}zdV\) 将积分改写为 \(\iiint_{\Omega}(2z+1)dV\)，此思路正确且有效。但在计算 \(I_1=2\iiint_{\Omega}zdV\) 时，积分区域投影选择 \(D_{zx}\) 并正确设置积分限，计算过程完整且结果正确（\(\frac{1}{6}\)）。计算 \(I_2=\iiint_{\Omega}dV\) 时，正确识别区域为三棱锥并应用体积公式，结果正确（\(\frac{1}{3}\)）。最终求和得 \(\frac{1}{2}\) 与标准答案一致。虽然方法与标准答案不同，但逻辑严谨且计算正确，得6分。

（3）最终结果（满分2分）

学生最终结果 \(\frac{1}{2}\) 完全正确，得2分。

题目总分：2+6+2=10分