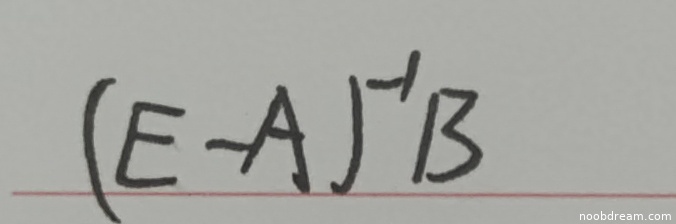
评分及理由

（1）得分及理由（满分5分）

学生给出的答案是 $(E - A)^{-1}B$，而标准答案是 $((E - (A - E)^{-1})^{-1}-E)A$。

从题目条件 $(E - (A - E)^{-1})B = A$ 出发，正确的解法应该是：

1. 将方程两边同时左乘 $(E - (A - E)^{-1})^{-1}$，得到 $B = (E - (A - E)^{-1})^{-1}A$

2. 然后计算 $B - A = (E - (A - E)^{-1})^{-1}A - A = [(E - (A - E)^{-1})^{-1} - E]A$

学生的答案 $(E - A)^{-1}B$ 与标准答案形式完全不同，且代入原方程验证不成立，说明存在逻辑错误。

此外，学生的答案中仍然包含未知矩阵 $B$，而题目要求的是 $B - A$ 的表达式，这进一步表明答案不正确。

因此，本题得分为0分。

题目总分：0分