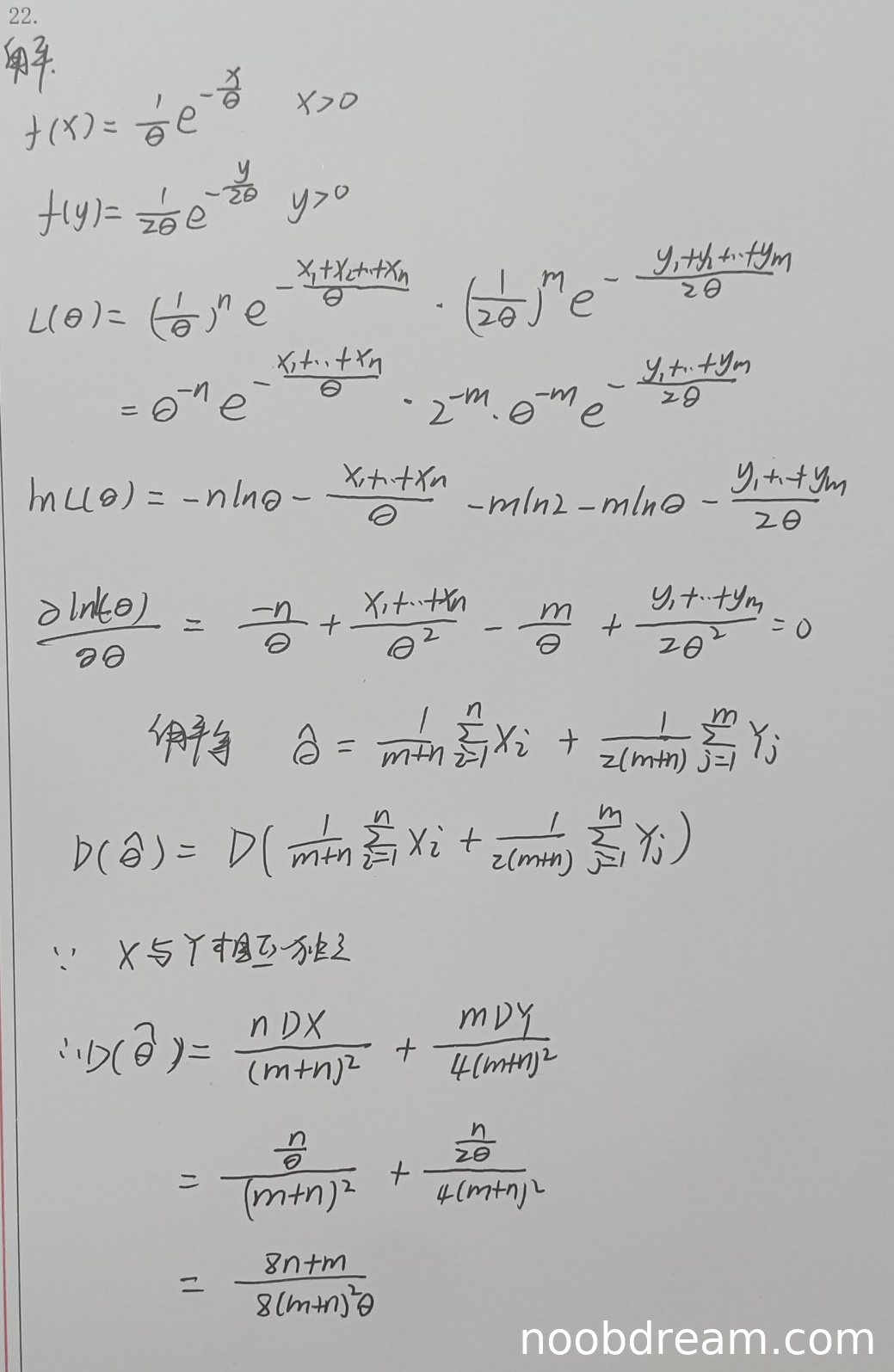
评分及理由

（1）得分及理由（满分6分）

学生正确写出了两个总体的概率密度函数，并构建了似然函数，取对数后求导，得到了最大似然估计量。虽然最终表达式与标准答案形式不同，但通过代数变换可以验证是等价的：

标准答案：$\hat{\theta}=\frac{2\sum X_i+\sum Y_j}{2(n+m)}$

学生答案：$\hat{\theta}=\frac{1}{m+n}\sum X_i+\frac{1}{2(m+n)}\sum Y_j$

两者实际上是相等的。思路完全正确，计算过程无误。得6分。

（2）得分及理由（满分6分）

学生在计算方差时存在严重错误：

1. 正确使用了方差的性质和独立性假设

2. 正确识别了$DX = \theta^2$，$DY = 4\theta^2$

3. 但在代入计算时出现了逻辑错误：

- 在$\frac{n\theta^2}{(m+n)^2}+\frac{m\times4\theta^2}{4(m+n)^2}$这一步是正确的

- 但接下来错误地写成了$\frac{n}{(m+n)^2}\theta+\frac{n}{4(m+n)^2}\times2\theta$，这里出现了两个错误：

* 将$\theta^2$误写为$\theta$

* 第二项分子出现了错误的$n$而不是$m$

4. 最终结果$\frac{8n+m}{8(m+n)^2}\theta$是错误的

由于存在明显的计算逻辑错误，扣3分。得3分。

题目总分：6+3=9分