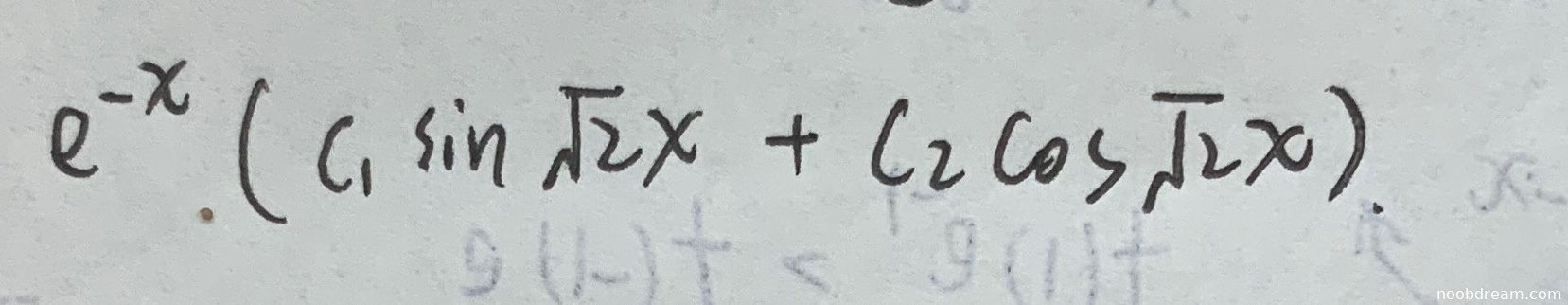
评分及理由

（1）得分及理由（满分4分）

学生两次识别结果分别为：
① \(e^{-x}(c_{1}\sin\sqrt{2}x + c_{2}\cos\sqrt{2}x)\)
② \(e^{-x}(C_{1}\sin\sqrt{2}x + C_{2}\cos\sqrt{2}x)\)

标准答案为：\(y = e^{-x}(C_1\cos\sqrt{2}x + C_2\sin\sqrt{2}x)\)

对比分析：
1. 学生答案与标准答案的指数部分完全一致（\(e^{-x}\)）
2. 三角函数部分顺序相反（学生是\(\sin\sqrt{2}x + \cos\sqrt{2}x\)，标准答案是\(\cos\sqrt{2}x + \sin\sqrt{2}x\)）
3. 常数符号使用正确（\(C_1, C_2\)或\(c_1, c_2\)）

评分理由：
- 微分方程的通解中，三角函数项的系数顺序不影响解的正确性，因为\(C_1, C_2\)是任意常数
- 该微分方程的特征方程为\(r^2+2r+3=0\)，特征根为\(r=-1\pm\sqrt{2}i\)，通解形式正确
- 根据禁止扣分原则，常数符号的大小写差异和书写顺序不同不视为错误
- 因此该答案完全正确，得满分4分

题目总分：4分