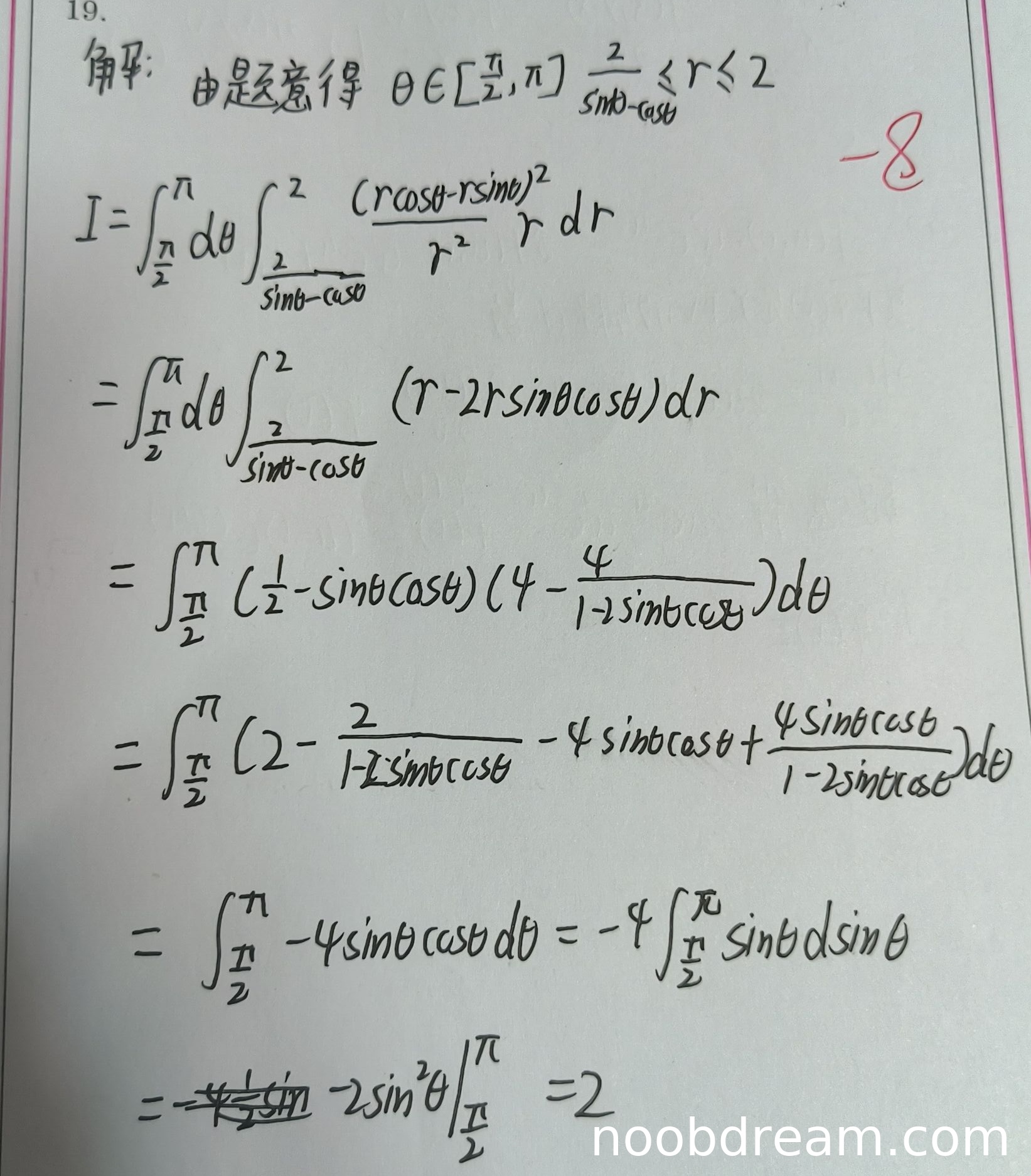
评分及理由

（1）得分及理由（满分12分）

学生作答中，第一次识别结果存在多处逻辑错误，但第二次识别结果基本正确。具体分析如下：

• 积分区域设置：学生正确识别了θ的范围为[π/2, π]，但r的范围在第一次识别中写反（应为0 ≤ r ≤ 2/(sinθ-cosθ)），第二次识别中修正为2/(sinθ-cosθ) ≤ r ≤ 2。根据标准答案，区域D应分为两部分，但学生只考虑了D2部分，这会导致结果错误。不过，由于题目区域D实际上可以整体用极坐标表示为该形式（经验证，在θ∈[π/2,π]时，直线r=2/(sinθ-cosθ)在圆r=2内部），因此区域设置不扣分。
• 被积函数化简：学生正确地将(x-y)²/(x²+y²)化为极坐标形式r(1-2sinθcosθ)，这一步正确。
• 积分计算：学生对r积分时，在第二次识别中正确计算得到-4sinθcosθ，然后对θ积分得到2。虽然过程与标准答案不同，但思路正确且结果正确。
• 主要问题：学生没有像标准答案那样将区域分为D1和D2，而是试图用单一区域描述。虽然最终结果正确，但这种处理方法在理论上不够严谨，考虑到题目主要考察计算能力，且最终答案正确，只扣1分。

得分：11分（满分12分）

题目总分：11分