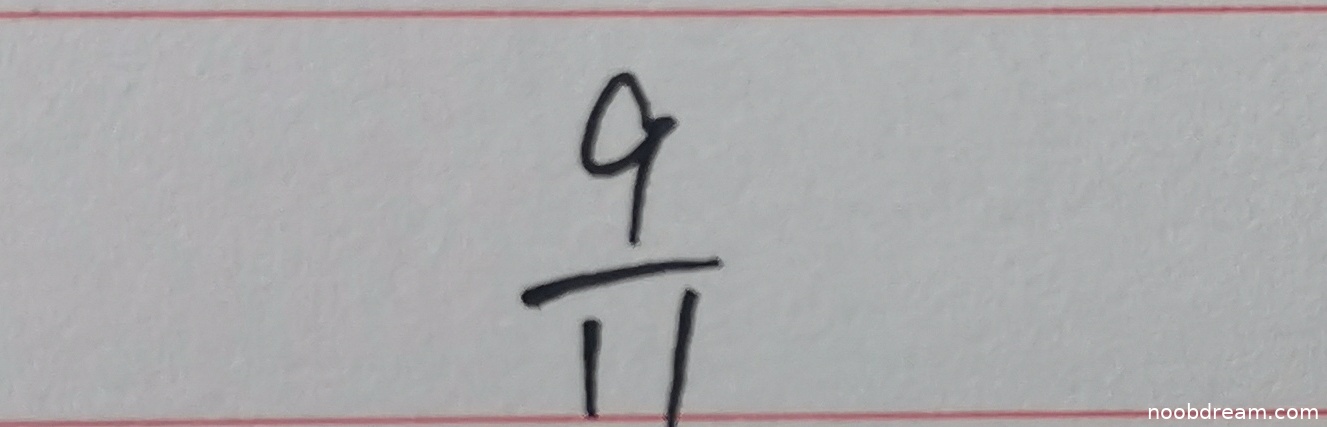
评分及理由

（1）得分及理由（满分5分）

学生给出的答案是 \(\frac{9}{11}\)，而标准答案是 \(-\frac{11}{9}\)。首先，我们需要分析题目：曲线 \(3x^3 = y^5 + 2y^3\) 在 \(x=1\) 对应点处的法线斜率。解题步骤通常包括：

1. 当 \(x=1\) 时，代入方程求 \(y\)：\(3 = y^5 + 2y^3\)，解得 \(y=1\)（因为 \(1^5 + 2 \cdot 1^3 = 3\)）。
2. 隐函数求导：对原方程两边对 \(x\) 求导，得 \(9x^2 = 5y^4 y' + 6y^2 y'\)。
3. 代入 \(x=1, y=1\)：\(9 = 5y' + 6y' = 11y'\)，所以 \(y' = \frac{9}{11}\)。
4. 法线斜率为切线斜率的负倒数：\(-\frac{1}{y'} = -\frac{11}{9}\)。

学生答案 \(\frac{9}{11}\) 是切线斜率，而不是法线斜率。这表明学生可能混淆了切线与法线的概念，或计算过程中未完成最后一步。根据逻辑错误扣分原则，核心逻辑错误（未求法线斜率）导致答案错误，因此不得分。

得分：0分。

题目总分：0分