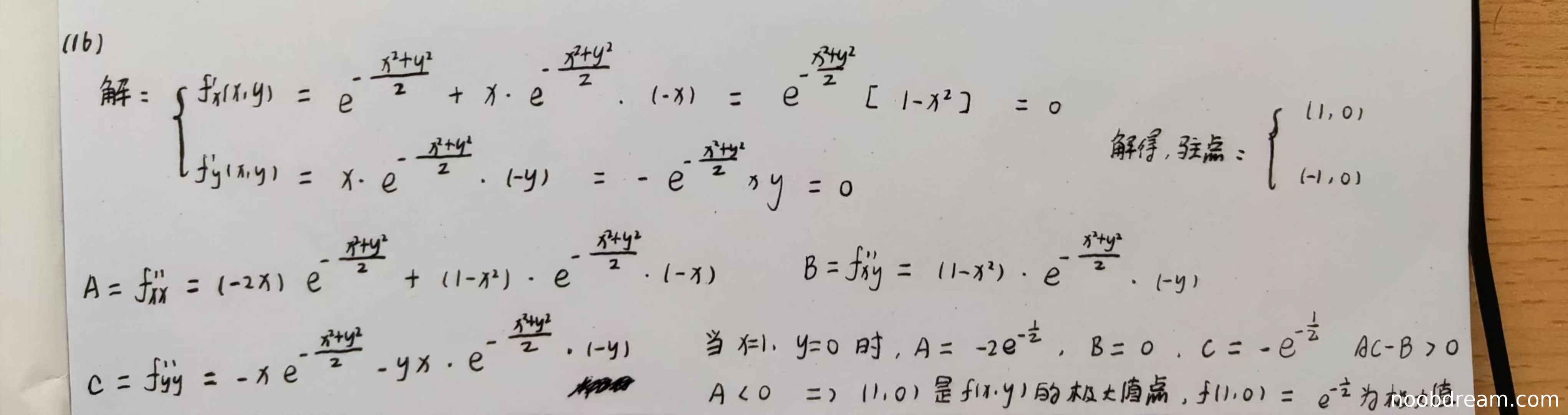
评分及理由

（1）驻点求解部分（满分3分）

学生正确计算了一阶偏导数并求解了驻点，得到(1,0)和(-1,0)。这部分完全正确，得3分。

（2）二阶偏导数计算部分（满分3分）

学生计算了A、B、C三个二阶偏导数：
- A的计算过程正确
- B的计算结果正确
- C的计算有误：标准答案为C = x(y²-1)e^{-(x²+y²)/2}，学生计算为C = -xe^{-(x²+y²)/2} - yx·e^{-(x²+y²)/2}·(-y)，这个表达式化简后不等于正确答案，存在逻辑错误。
由于二阶偏导数计算有误，扣1分，得2分。

（3）极值判断部分（满分4分）

学生只对(1,0)点进行了判断：
- 代入数值计算A、B、C时，虽然C的计算公式有误，但代入x=1,y=0后得到C=-e^{-1/2}，这个数值结果碰巧正确
- 正确计算了AC-B²>0且A<0，判断(1,0)为极大值点
- 但未对(-1,0)点进行判断，这是明显的遗漏
由于遗漏了对(-1,0)点的判断，扣2分，得2分。

题目总分：3+2+2=7分