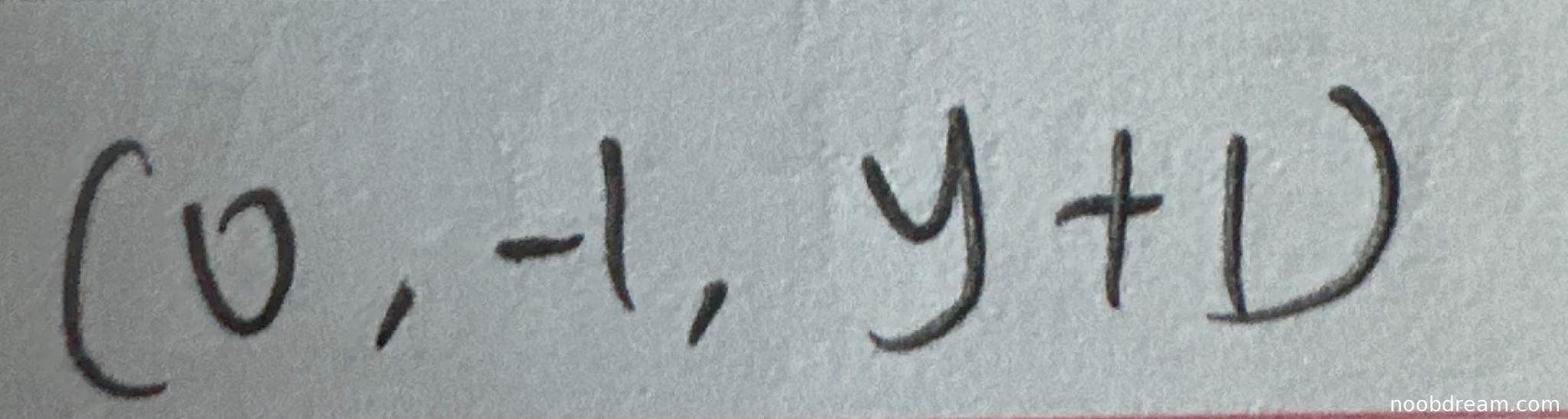
评分及理由

（1）得分及理由（满分4分）

向量场的旋度计算公式为： \[ \text{rot}\boldsymbol{A} = \left( \frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z}, \frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x}, \frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} \right) \] 其中 \(\boldsymbol{A} = (x+y+z, xy, z)\)。计算各分量： - 第一分量：\(\frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z} = \frac{\partial z}{\partial y} - \frac{\partial (xy)}{\partial z} = 0 - 0 = 0\) - 第二分量：\(\frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x} = \frac{\partial (x+y+z)}{\partial z} - \frac{\partial z}{\partial x} = 1 - 0 = 1\) - 第三分量：\(\frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} = \frac{\partial (xy)}{\partial x} - \frac{\partial (x+y+z)}{\partial y} = y - 1\)

标准答案为 \((0, 1, y-1)\)，学生答案为 \((0, -1, y+1)\)。第二分量应为1但学生得到-1，第三分量应为\(y-1\)但学生得到\(y+1\)。这两个分量的计算存在明显的逻辑错误，不符合旋度的定义和计算规则。因此本题得0分。

题目总分：0分