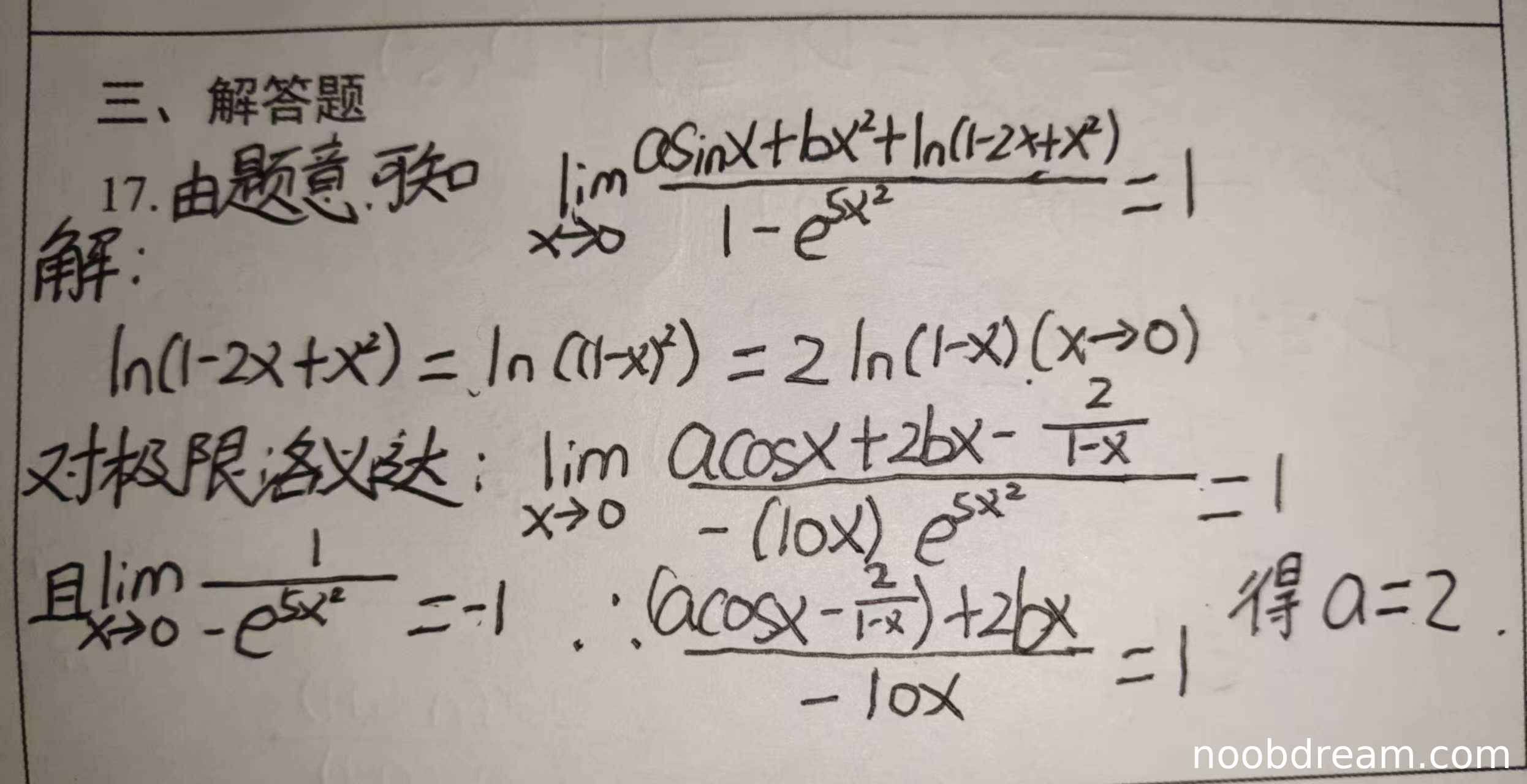
评分及理由

（1）得分及理由（满分10分）

学生正确写出等价无穷小条件：\(\lim_{x \to 0} \frac{a\sin x + bx^2 + \ln(1 - 2x + x^2)}{1 - e^{5x^2}} = 1\)，得1分。

学生将\(\ln(1 - 2x + x^2)\)化简为\(2\ln(1 - x)\)，这一步正确，得1分。

学生使用洛必达法则求导，分子导数正确为\(a\cos x + 2bx - \frac{2}{1-x}\)，分母导数正确为\(-10xe^{5x^2}\)，得2分。

学生注意到\(\lim_{x \to 0} \frac{1}{-e^{5x^2}} = -1\)，这一步正确，得1分。

学生得到方程\(\frac{(a\cos x - \frac{2}{1-x}) + 2bx}{-10x} = 1\)，但此处逻辑有误：未考虑极限过程，直接令表达式等于1，扣1分。

学生得出\(a = 2\)，结果正确，但推导过程不严谨（未展开极限计算），扣1分。

学生未求出b的值，扣3分。

小计得分：1+1+2+1-1-1-3 = 0分

题目总分：0分