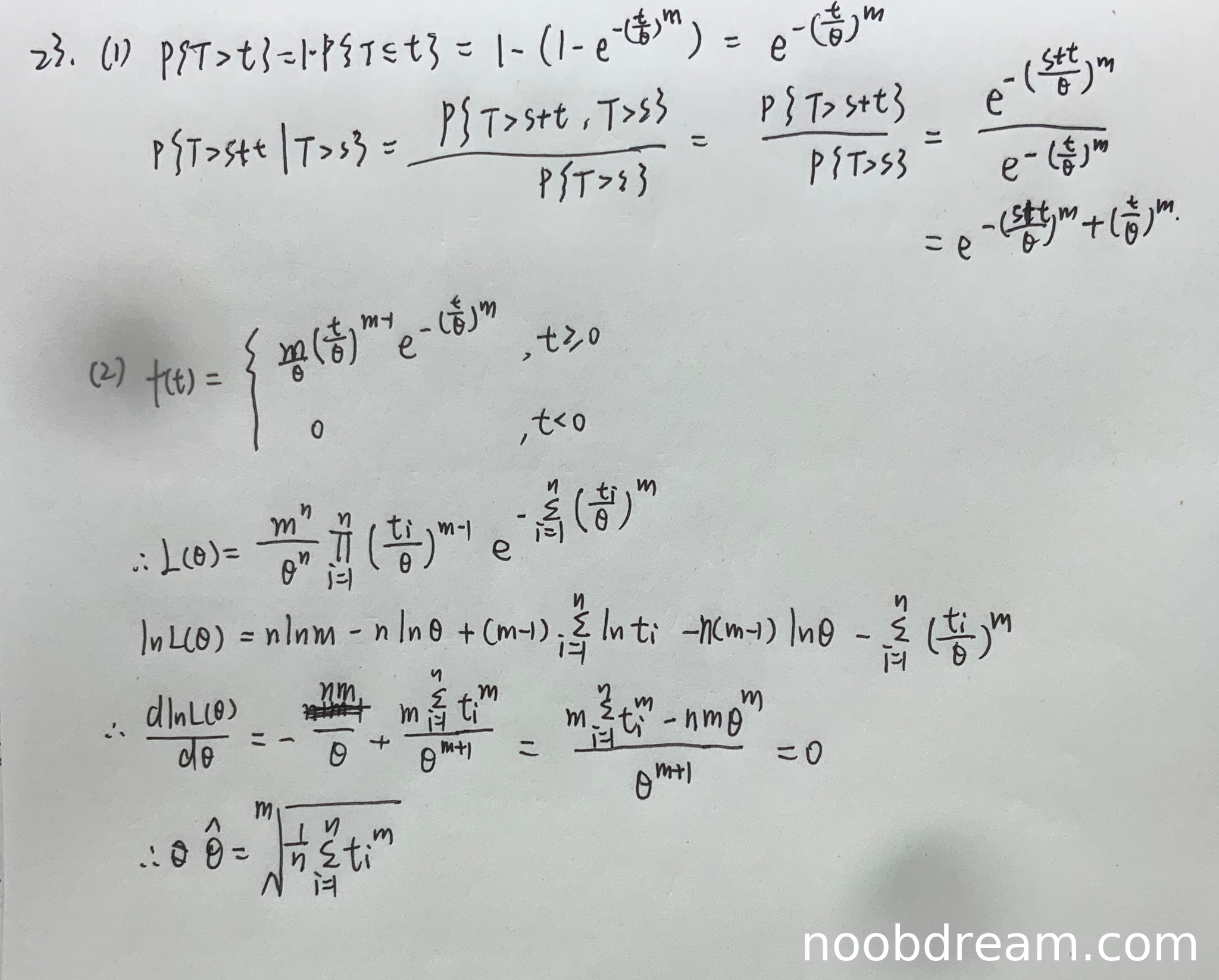
评分及理由

（1）得分及理由（满分5.5分）

第一问包含两个小问：

• 对于 \(P\{T>t\}\)：学生正确计算出结果为 \(e^{-(\frac{t}{\theta})^m}\)，与标准答案一致，得满分部分（通常占该问的一半分值，即2.75分）。
• 对于 \(P\{T>s+t | T>s\}\)：学生正确应用条件概率公式并化简得到 \(e^{-(\frac{s+t}{\theta})^m + (\frac{s}{\theta})^m}\)，但在指数部分书写为“- ... -”的形式（第一次识别结果）或“- ... +”的形式（第二次识别结果）。第二次识别结果中的表达式 \(e^{-(\frac{s+t}{\theta})^m + (\frac{s}{\theta})^m}\) 等价于标准答案的 \(e^{\frac{s^m - (s+t)^m}{\theta^m}}\)，因为指数运算中减法在分母上体现为指数相减。因此，核心逻辑正确，仅书写形式略有差异，不扣分。该部分得满分（2.75分）。

第一问总分：2.75 + 2.75 = 5.5分。

（2）得分及理由（满分5.5分）

第二问包含概率密度函数、似然函数构建、对数似然函数求导及求解估计值：

• 概率密度函数 \(f(t)\)：学生正确给出 \(f(t) = \frac{m}{\theta}(\frac{t}{\theta})^{m-1}e^{-(\frac{t}{\theta})^m}\)（与标准答案等价），得满分部分（通常占该问的1/4分值，即1.375分）。
• 似然函数 \(L(\theta)\)：学生正确构建为 \(L(\theta) = \frac{m^n}{\theta^n} \prod_{i=1}^n (\frac{t_i}{\theta})^{m-1} e^{-\sum_{i=1}^n (\frac{t_i}{\theta})^m}\)，与标准答案一致，得满分部分（1.375分）。
• 对数似然函数 \(\ln L(\theta)\)：学生正确写出为 \(n\ln m - n\ln\theta + (m-1)\sum \ln t_i - n(m-1)\ln\theta - \sum (\frac{t_i}{\theta})^m\)，其中 \(-n\ln\theta - n...