评分及理由

（1）得分及理由（满分2分）

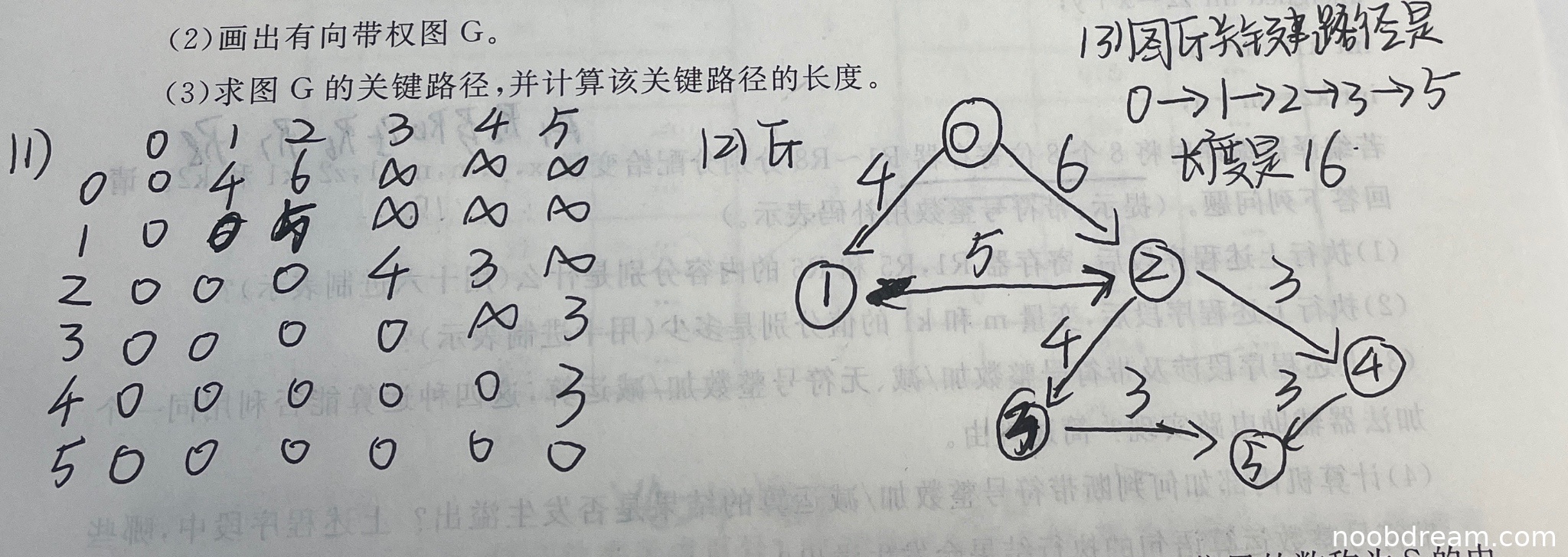
学生给出的邻接矩阵为：

0  4  6  ∞  ∞  ∞
4  0  5  ∞  ∞  ∞
6  5  0  4  3  ∞
∞  ∞  4  0  ∞  3
∞  ∞  3  ∞  0  3
∞  ∞  ∞  3  3  0

标准答案为上三角矩阵，且对角线为0。学生答案中出现了下三角元素（如A[1][0]=4, A[2][0]=6, A[2][1]=5等），这与题目给定的上三角矩阵条件不符。邻接矩阵构建错误，但部分上三角元素（如A[0][1]=4, A[0][2]=6, A[1][2]=5, A[2][3]=4, A[2][4]=3, A[3][5]=3, A[4][5]=3）正确。由于核心逻辑错误（未按上三角矩阵构建），扣1分。

得分：1分

（2）得分及理由（满分2分）

学生提到"有向带权图（图中已画出）"，但识别结果中未提供具体图形。由于无法判断图形是否正确，且邻接矩阵存在错误，推测图形可能基于错误的邻接矩阵绘制。根据邻接矩阵部分正确元素，可能画出部分正确边，但整体结构错误。扣1分。

得分：1分

（3）得分及理由（满分4分）

学生给出的关键路径为0→1→2→3→5，长度为16，与标准答案完全一致。虽然邻接矩阵构建错误，但关键路径计算正确，说明学生可能通过其他方式（如直接分析边权）得出正确结果。按照"思路正确不扣分"原则，不因邻接矩阵错误而扣减本题分数。

得分：4分

题目总分：1+1+4=6分