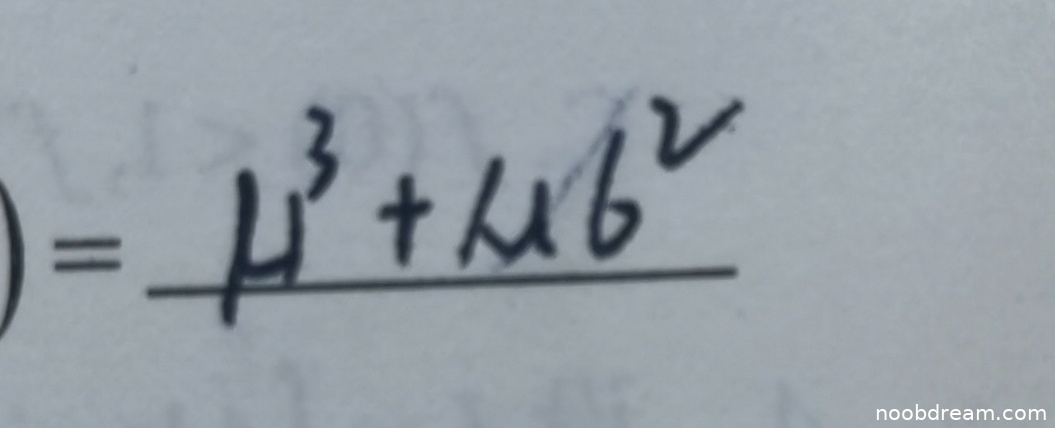
评分及理由

（1）得分及理由（满分4分）

学生作答的识别结果为：$=\frac{\mu^{3}+\mu b^{2}}{}$。根据题目条件，二维随机变量服从 $N(\mu, \mu ; \sigma^{2}, \sigma^{2} ; 0)$，即 $X$ 和 $Y$ 独立同分布，均服从 $N(\mu, \sigma^2)$，且相关系数为0。

计算 $E(XY^2)$：由于 $X$ 和 $Y$ 独立，$E(XY^2) = E(X)E(Y^2)$。其中 $E(X) = \mu$，$E(Y^2) = Var(Y) + [E(Y)]^2 = \sigma^2 + \mu^2$。因此 $E(XY^2) = \mu(\sigma^2 + \mu^2) = \mu^3 + \mu\sigma^2$。

学生答案中 $\mu^{3}+\mu b^{2}$ 与标准答案 $\mu^{3}+\mu\sigma^{2}$ 对比，识别结果中的 $b$ 很可能是 $\sigma$ 的误写（因为 $b$ 与 $\sigma$ 形状相似，且上下文是概率论题目，$\sigma$ 是标准符号）。根据禁止扣分规则第1条和第4条，字符识别错误导致的误写不扣分。核心逻辑正确，分子部分与标准答案一致，分母为空可能是识别不全，但不影响主要结果判断。

因此给满分4分。

题目总分：4分