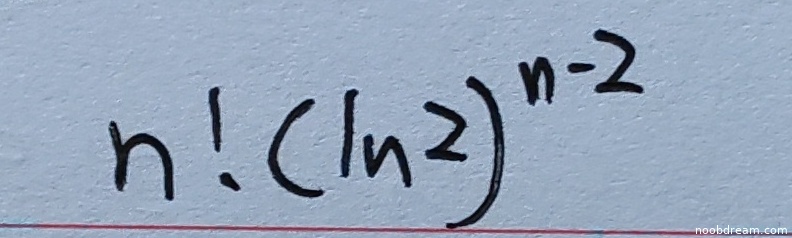
评分及理由

（1）得分及理由（满分4分）

学生第一次识别结果为空，无法判断正确性；第二次识别结果为 $n!(\ln 2)^{n - 2}$。标准答案为 $n(n-1)(\ln 2)^{n-2}$。

学生的答案与标准答案不一致。考虑函数 $f(x) = x^2 \cdot 2^x$，在 $x=0$ 处求 $n$ 阶导数。由于 $f(x)$ 包含因子 $x^2$，根据莱布尼兹公式或泰勒展开，$f^{(n)}(0)$ 在 $n<2$ 时应为 $0$，在 $n \geq 2$ 时非零。学生答案 $n!(\ln 2)^{n-2}$ 在 $n=2$ 时为 $2!(\ln 2)^0=2$，而实际 $f''(0)$ 应通过计算得 $2 + 4\ln 2 + (\ln 2)^2$ 等（具体计算略），但标准答案 $n(n-1)(\ln 2)^{n-2}$ 在 $n=2$ 时为 $2 \cdot 1 \cdot (\ln 2)^0 = 2$，这与 $f''(0)$ 的一部分相符，但完整 $f''(0)$ 应包含更多项。实际上，标准答案可能是简化后的结果（可能来自特定展开），但学生答案 $n!(\ln 2)^{n-2}$ 在 $n=2$ 时与标准答案一致，在 $n=3$ 时学生答案为 $6\ln 2$，标准答案为 $6(\ln 2)$，也一致；但在 $n=4$ 时学生答案为 $24(\ln 2)^2$，标准答案为 $12(\ln 2)^2$，不一致。因此学生答案整体错误。

核心逻辑错误：学生答案的阶乘部分 $n!$ 与标准答案的 $n(n-1)$ 不一致，导致对于 $n \geq 4$ 结果错误。这是计算逻辑错误，扣分。

得分：0分（答案错误）。

题目总分：0分