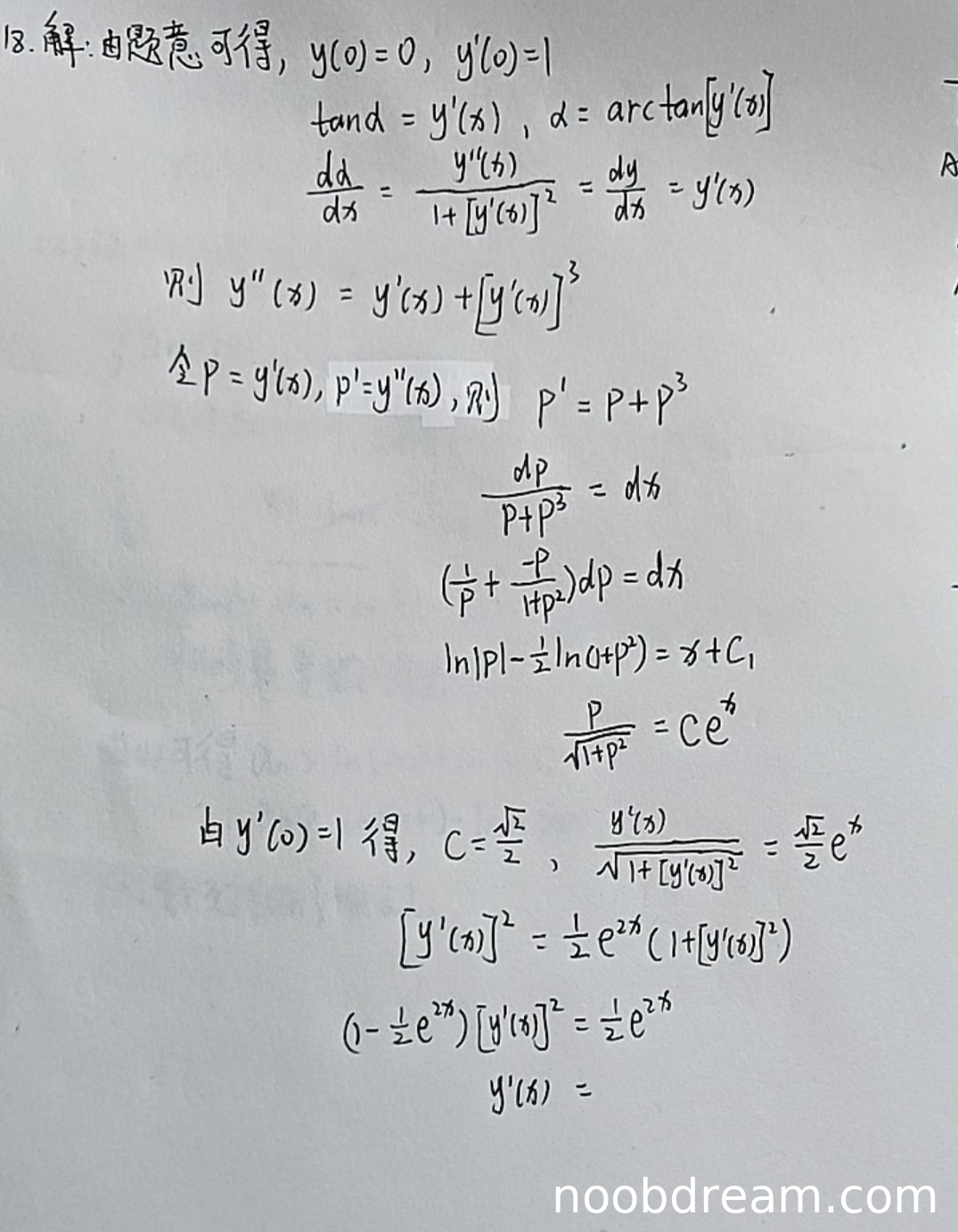
评分及理由

（1）得分及理由（满分10分）

学生正确写出初始条件 \( y(0) = 0 \)、\( y'(0) = 1 \)（1分）。正确建立 \(\tan\alpha = y'(x)\) 并推导出 \(\frac{d\alpha}{dx} = \frac{y''(x)}{1 + [y'(x)]^2}\)（2分）。正确代入条件 \(\frac{d\alpha}{dx} = \frac{dy}{dx}\) 得到微分方程 \(y''(x) = y'(x) + [y'(x)]^3\)（2分）。正确令 \(P = y'(x)\) 并化为 \(\frac{dP}{P + P^3} = dx\)（1分）。积分过程正确得到 \(\ln|P| - \frac{1}{2}\ln(1 + P^2) = x + C_1\)（1分）。正确代入初始条件 \(y'(0) = 1\) 解得 \(C = \frac{\sqrt{2}}{2}\)（1分）。但最终未解出 \(y(x)\) 的表达式，且最后一步代数运算未完成（扣2分）。

题目总分：1+2+2+1+1+1-2=6分