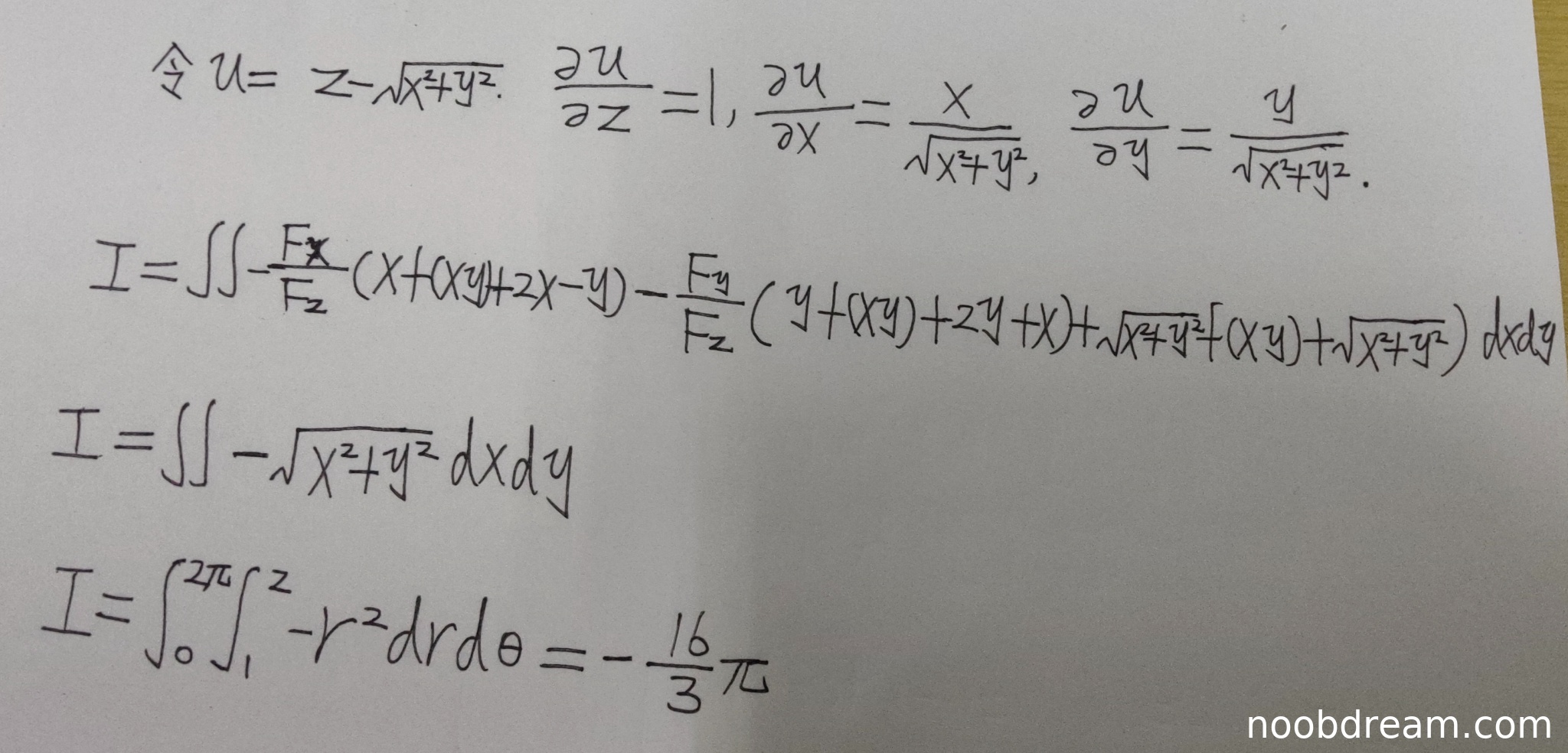
评分及理由

（1）变量设定与求偏导部分（满分2分）

得分：1分

理由：学生正确设定了曲面方程 \(u = z-\sqrt{x^{2}+y^{2}}\)，但在计算偏导数时出现错误。标准答案为 \(F_x' = -\frac{x}{\sqrt{x^{2}+y^{2}}}\)，而学生得到 \(\frac{x}{\sqrt{x^{2}+y^{2}}}\)（缺少负号）。这是一个关键的计算错误，扣1分。

（2）曲面积分转换部分（满分4分）

得分：2分

理由：学生正确应用了曲面积分转换为二重积分的方法，但在具体计算时存在多处错误：

• 被积函数中 \(f(xy)\) 项的处理不完整
• 符号错误（由于偏导数错误导致整体符号错误）
• 最终化简结果 \(-\sqrt{x^{2}+y^{2}}\) 缺少绝对值或方向处理

虽然思路正确，但计算过程存在严重错误，扣2分。

（3）极坐标计算部分（满分4分）

得分：1分

理由：

• 正确识别了积分区域为圆环区域 \(1 \leq r \leq 2\)，\(0 \leq \theta \leq 2\pi\)
• 正确进行了极坐标变换 \(dxdy = rdrd\theta\)
• 但积分计算错误：\(\int_{1}^{2}-r^{2}dr = -\frac{7}{3}\) 正确，但最终结果 \(-\frac{16}{3}\pi\) 计算错误（应为 \(-\frac{14}{3}\pi\)）
• 由于方向处理错误（曲面为下侧，应在转换时考虑符号），最终结果符号也错误

扣3分。

题目总分：1+2+1=4分