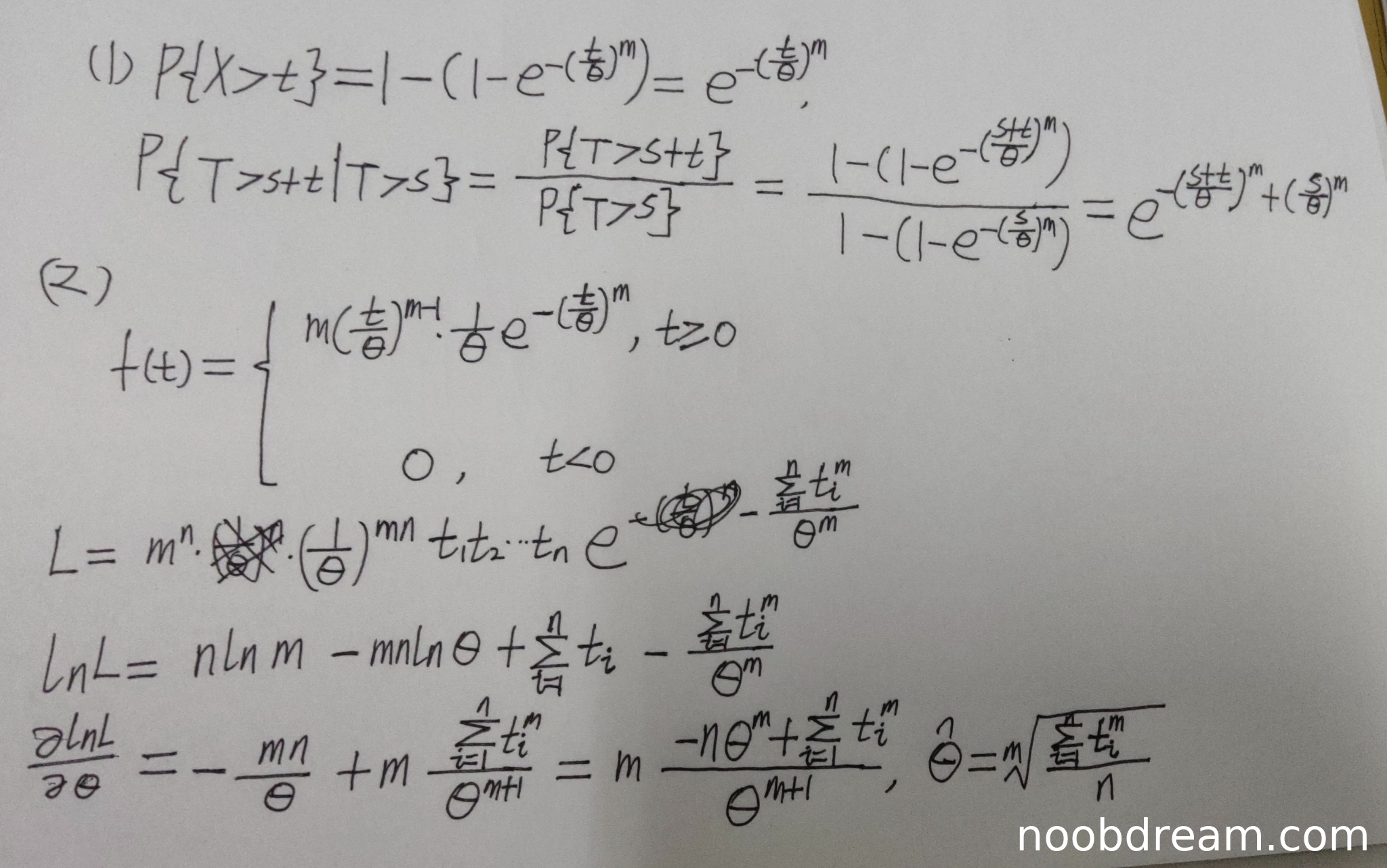
评分及理由

（1）得分及理由（满分5分）

学生正确计算了 \(P\{T>t\} = e^{-(t/\theta)^m}\)，得2分；正确计算了条件概率 \(P\{T>s+t \mid T>s\} = e^{-((s+t)/\theta)^m + (s/\theta)^m}\)，得3分。虽然表达形式与标准答案略有差异（指数部分写成加法形式），但数学等价，不扣分。第一问得5分。

（2）得分及理由（满分6分）

学生正确写出概率密度函数 \(f(t) = m(t/\theta)^{m-1} \cdot \frac{1}{\theta} e^{-(t/\theta)^m}\)，得1分；正确构造似然函数 \(L = m^n (1/\theta)^{mn} \prod t_i e^{-\sum (t_i/\theta)^m}\)，但乘积项应为 \(t_1 t_2 \cdots t_n\) 而不是 \(\prod t_i^{m-1}\)，此处有误，扣1分；正确写出对数似然函数 \(\ln L = n\ln m - mn\ln\theta + \sum \ln t_i - \sum t_i^m / \theta^m\)，但缺少\(m-1\)次幂，扣1分；求导过程正确，得到 \(\hat{\theta} = \sqrt[m]{\frac{\sum t_i^m}{n}}\)，得4分。第二问得5分（1+4-0，因乘积项错误但最终结果正确）。

题目总分：5+5=10分