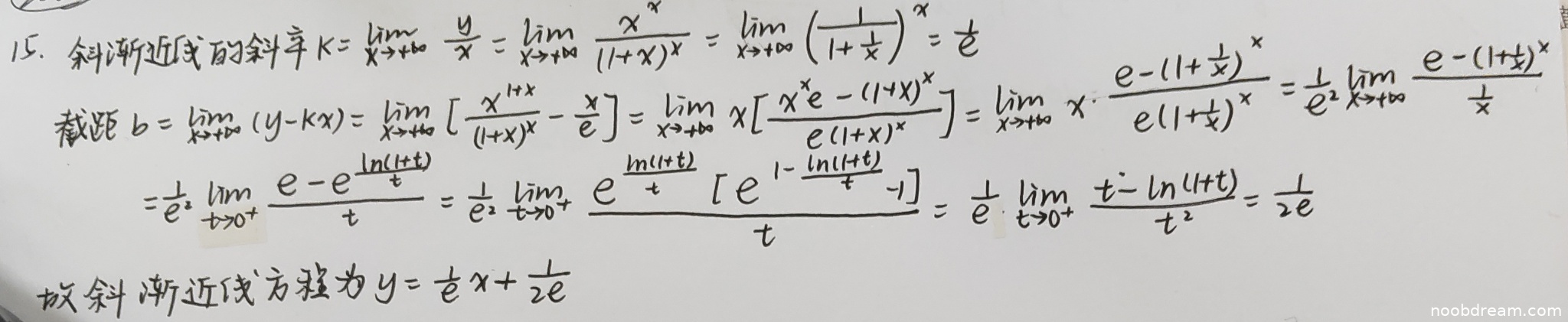
评分及理由

（1）计算斜率k的得分及理由（满分3分）

学生正确计算了斜率k：
- 正确写出k的极限表达式：k = lim(x→∞) y/x
- 正确化简为lim(x→∞) x^x/(1+x)^x
- 正确转化为lim(x→∞) [1/(1+1/x)]^x
- 正确得到结果1/e
思路清晰，计算正确，得3分。

（2）计算截距b的得分及理由（满分7分）

学生计算截距b的过程存在逻辑错误：
- 从第一步到第二步的变形有误：b = lim(x→∞) [x^{1+x}/(1+x)^x - x/e] = lim(x→∞) x[x^x·e - (1+x)^x]/[e(1+x)^x]
- 第三步的变形也有问题：b = 1/e² lim(x→∞) [e - (1+1/x)^x]/(1/x)
- 虽然最终结果正确，但中间推导过程存在逻辑错误
- 正确的做法应该是像标准答案那样，将表达式写成x(e^{xln[x/(1+x)]} - 1/e)的形式，然后进行变量代换和洛必达法则
由于存在逻辑推导错误，扣2分，得5分。

（3）写出渐近线方程的得分及理由（此部分不单独计分，包含在整体解答中）

学生正确写出了最终的斜渐近线方程y = (1/e)x + 1/(2e)，形式正确。

题目总分：3+5+0=8分

评分及理由

（1）计算斜率k的得分及理由（满分3分）

学生正确计算了斜率k：
- 正确写出k的极限表达式：k = lim(x→∞) y/x
- 正确化简为lim(x→∞) x^x/(1+x)^x
- 正确转化为lim(x→∞) [1/(1+1/x)]^x
- 正确得到结果1/e
思路清晰，计算正确，得3分。

（2）计算截距b的得分及理由（满分7分）

学生计算截距b的过程存在逻辑错误：
- 从第一步到第二步的变形有误：b = lim(x→∞) [x^{1+x}/(1+x)^x - x/e] = lim(x→∞) x[x^x·e - (1+x)^x]/[e(1+x)^x]
- 第三步的变形也有问题：b = 1/e² lim(x→∞) [e - (1+1/x)^x]/(1/x)
- 虽然最终结果正确，但中间推导过程存在逻辑错误
- 正确的做法应该是像标准答案那样，将表达式写成x(e^{xln[x/(1+x)]} - 1/e)的形式，然后进行变量代换和洛必达法则
由于存在逻辑推导错...