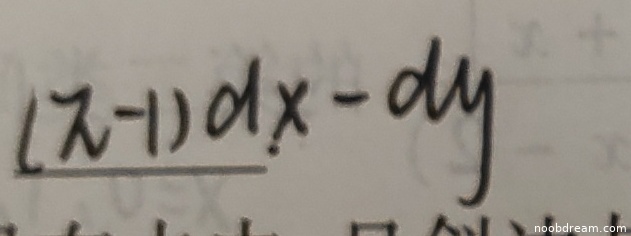
评分及理由

（1）得分及理由（满分4分）

学生给出的答案是 $(x - 1)dx - dy$，而标准答案是 $(\pi-1) d x-d y$。

计算全微分 $dz$ 需要求出偏导数 $\frac{\partial z}{\partial x}$ 和 $\frac{\partial z}{\partial y}$ 在点 $(0, \pi)$ 处的值。

设 $u = xy + \sin(x+y)$，则 $z = \arctan u$，$\frac{\partial z}{\partial x} = \frac{1}{1+u^2} \cdot \frac{\partial u}{\partial x}$，$\frac{\partial u}{\partial x} = y + \cos(x+y)$。

在点 $(0, \pi)$ 处，$u = 0\cdot\pi + \sin(0+\pi) = 0$，$\frac{\partial u}{\partial x} = \pi + \cos(\pi) = \pi - 1$，所以 $\frac{\partial z}{\partial x} = \frac{1}{1+0} \cdot (\pi-1) = \pi-1$。

同理，$\frac{\partial u}{\partial y} = x + \cos(x+y)$，在 $(0, \pi)$ 处为 $0 + \cos(\pi) = -1$，所以 $\frac{\partial z}{\partial y} = \frac{1}{1+0} \cdot (-1) = -1$。

因此 $dz|_{(0,\pi)} = (\pi-1)dx - dy$。

学生答案中写的是 $(x - 1)dx - dy$，将 $\pi$ 误写为 $x$。根据禁止扣分规则第1条和第4条，由于字符相似（$\pi$ 和 $x$ 在识别中可能混淆），且这是明显的误写而非逻辑错误，因此不扣分。学生的答案在结构上与标准答案一致，只是符号误写。

得分为4分。

题目总分：4分