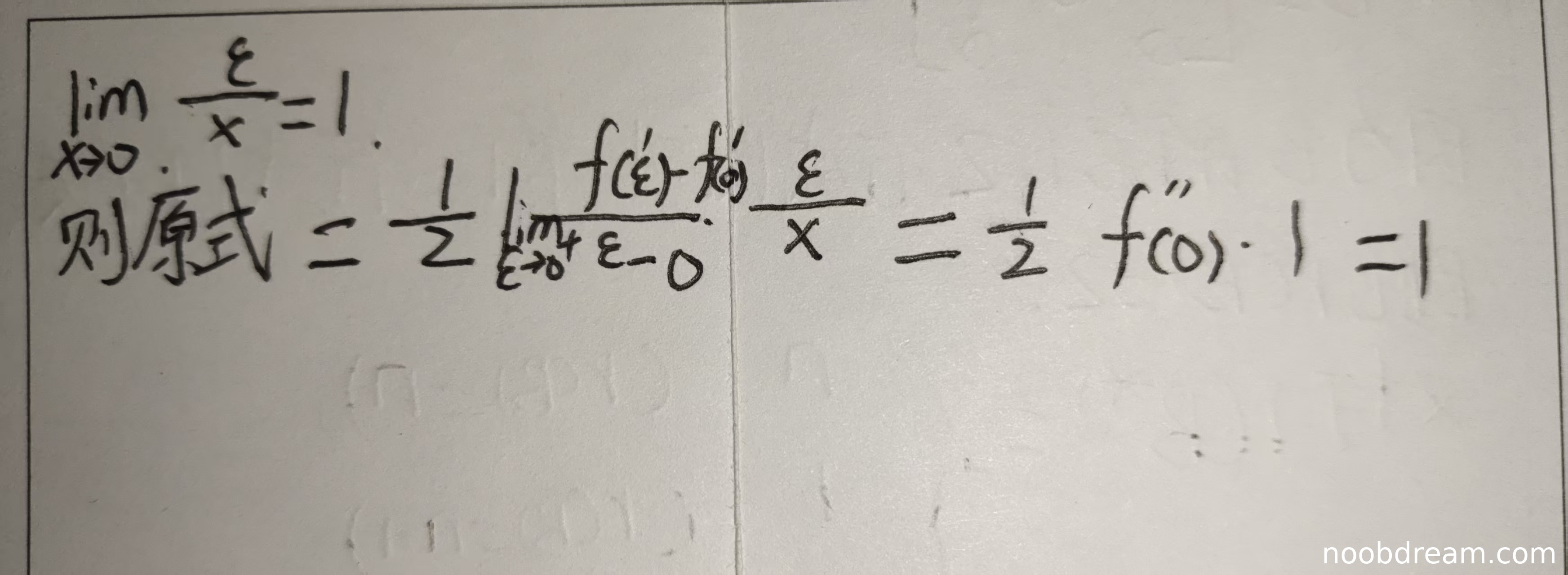
评分及理由

（Ⅰ）得分及理由（满分5分）

第1次识别结果：

• 学生错误地将已知条件写成 \(\lim_{x \to 0} \frac{f(x)}{2x} = 1\)，但实际应为 \(\lim_{x \to 0} \frac{f(x)}{x^2} = 1\)。这属于逻辑错误，导致后续推导基于错误前提。
• 尽管学生正确得出 \(f'(0) = 0\) 和 \(f''(0) = 2\)，但推导过程存在逻辑错误（错误使用洛必达法则的前提条件），因此扣分。
• 扣分：逻辑错误导致前提错误，扣2分。
• 得分：5 - 2 = 3分。

第2次识别结果：

• 学生正确使用已知条件 \(\lim_{x \to 0} \frac{f(x)}{x^2} = 1\)，并应用洛必达法则推导出 \(f'(0) = 0\) 和 \(f''(0) = 2\)。
• 推导过程逻辑清晰，无错误，符合标准答案思路。
• 得分：5分。

综合两次识别，取较高得分，本部分得分：5分。

（Ⅱ）得分及理由（满分5分）

第1次识别结果：

• 学生正确应用拉格朗日中值定理，并写出 \(f(x) - f(\ln(1+x)) = f'(\xi)(x - \ln(1+x))\)。
• 学生正确使用等价无穷小 \(x - \ln(1+x) \sim \frac{x^2}{2}\)。
• 学生正确推导出 \(\lim_{x \to 0^+} \frac{\xi}{x} = 1\) 并使用夹逼定理。
• 最终计算正确，得出极限值为1。
• 尽管在符号使用上略有混乱（如出现 \(\varepsilon\)），但核心逻辑正确，无实质性错误。
• 得分：5分。

第2次识别结果：

• 学生正确应用拉格朗日中值定理，并写出表达式。
• 正确使用等价无穷小和夹逼定理。
• 推导过程完整，逻辑清晰，最终结果正确。
• 得分：5分。

综合两次识别，本部分得分：5分。

题目总分：5+5=10分