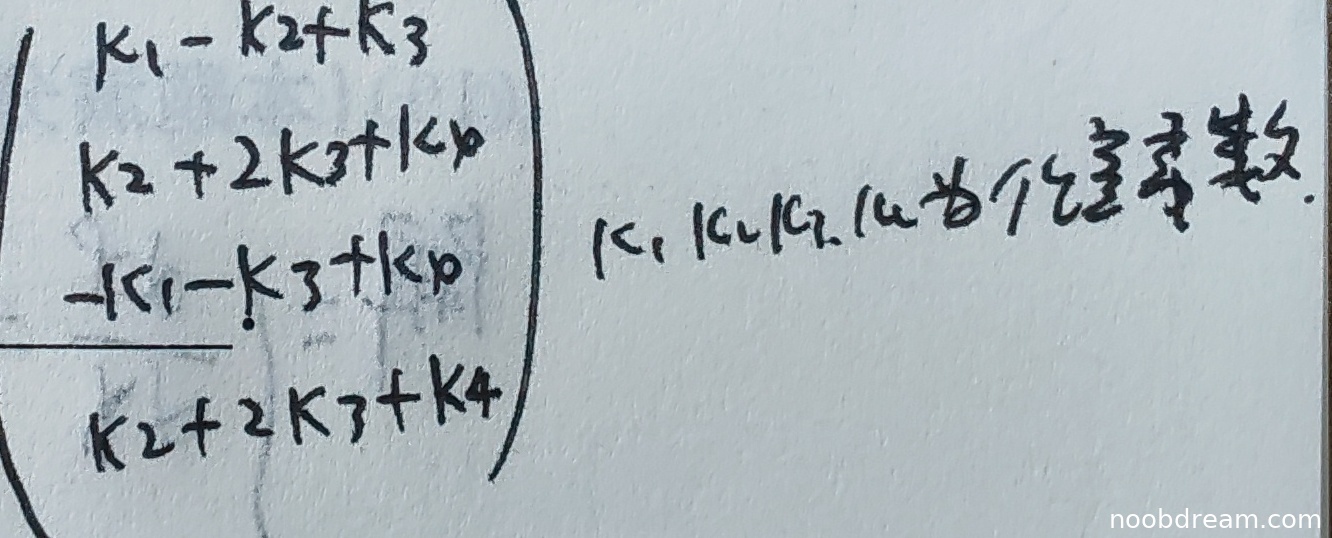
评分及理由

（1）得分及理由（满分5分）

学生作答得分为0分。

理由：题目要求求解齐次方程组 \(\begin{pmatrix}A\\B\end{pmatrix}x = 0\) 的解，即同时满足 \(Ax=0\) 和 \(Bx=0\) 的解向量。学生给出的答案是一个含有四个自由参数 \(k_1, k_2, k_3, k_4\) 的向量形式，这表明学生可能试图将 \(A\) 和 \(B\) 的解空间直接合并或线性组合，但未正确理解两个方程组联立的解应是它们各自解空间的交集（即公共解）。标准答案是一个仅含一个自由参数 \(k\) 的向量，表示解空间是一维的。学生的答案维度错误（给出了四维解空间，而实际应为一维），且未正确求出公共解，因此逻辑错误，得0分。

题目总分：0分