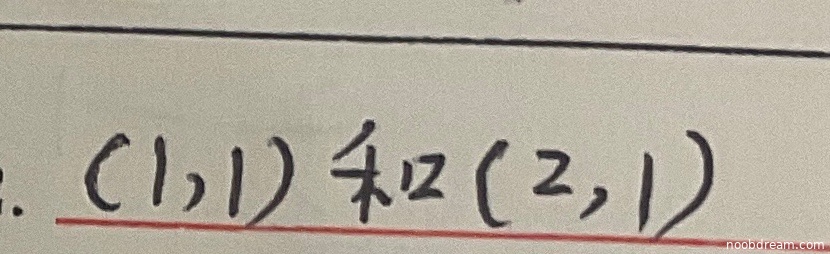
评分及理由

（1）得分及理由（满分5分）

学生作答给出了两个点：(1,1)和(2,1)。标准答案是(1,1)。对于多元函数求极值点，需要先求偏导数并解方程组找到驻点，然后利用二阶导数检验判断是否为极值点。函数$f(x,y)=2x^3-9x^2-6y^4+12x+24y$的偏导数为：

• $f_x=6x^2-18x+12=6(x^2-3x+2)=6(x-1)(x-2)$
• $f_y=-24y^3+24=-24(y^3-1)=-24(y-1)(y^2+y+1)$

令偏导数为零，解得驻点为$(1,1)$和$(2,1)$。但需要进一步判断是否为极值点：

• 在$(1,1)$处，$f_{xx}=12x-18=-6$，$f_{yy}=-72y^2=-72$，$f_{xy}=0$，判别式$D=f_{xx}f_{yy}-(f_{xy})^2=432>0$且$f_{xx}<0$，故为极大值点。
• 在$(2,1)$处，$f_{xx}=6$，$f_{yy}=-72$，$f_{xy}=0$，判别式$D=-432<0$，故不是极值点。

因此只有$(1,1)$是极值点。学生作答包含了非极值点$(2,1)$，属于逻辑错误，但根据题目要求，填空题应只填写极值点，多写错误点应扣分。考虑到识别可能误写，但这里两个点都清晰写出，不属于误写。因此扣2分，得3分。

题目总分：3分