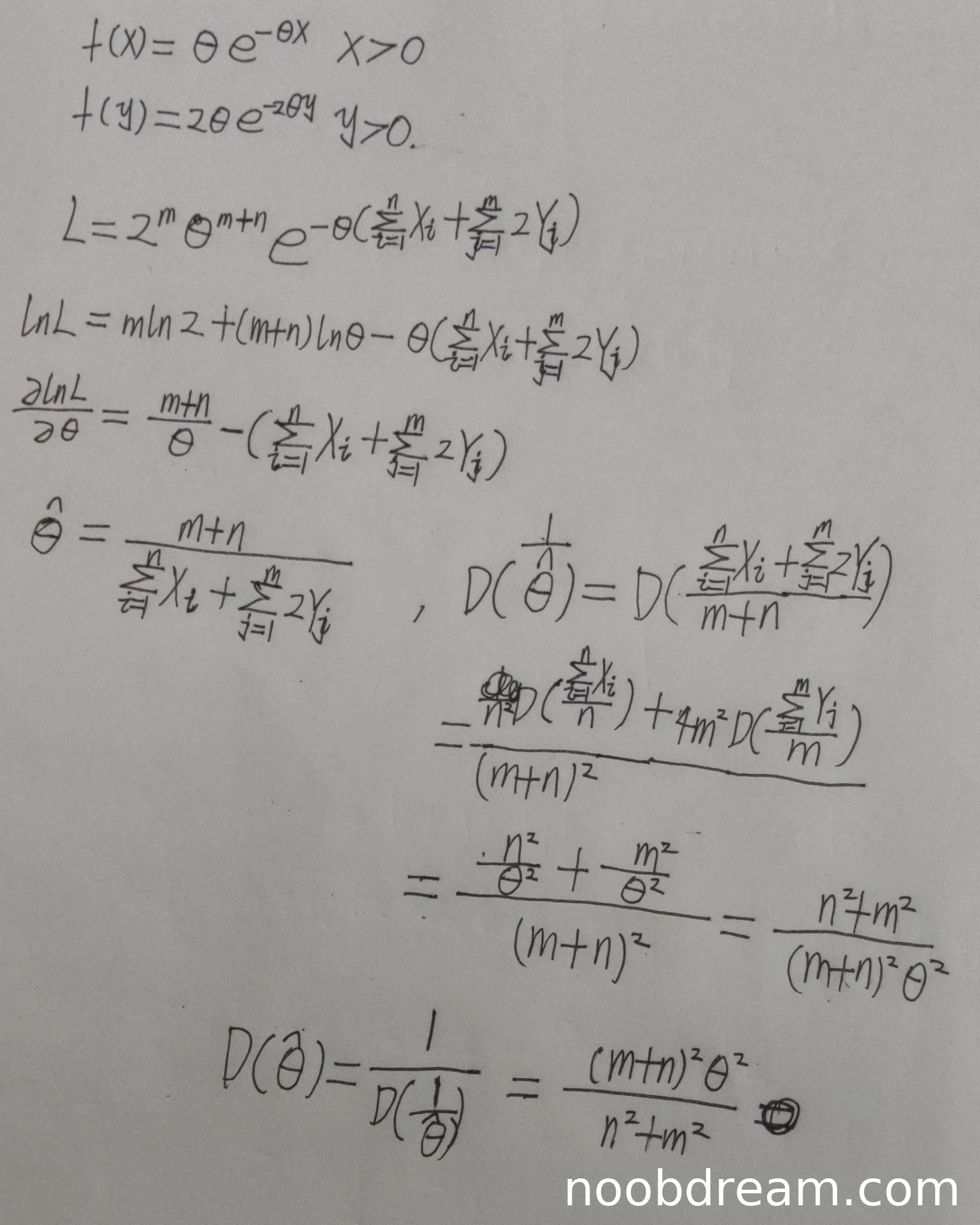
评分及理由

（1）得分及理由（满分6分）

学生给出的概率密度函数形式与标准答案不一致：标准答案中X的密度为(1/θ)e^(-x/θ)，学生写为θe^(-θx)；Y的密度为(1/(2θ))e^(-y/(2θ))，学生写为2θe^(-2θy)。这导致后续似然函数构建错误。虽然学生按照最大似然估计的步骤进行了推导，但由于密度函数形式错误，导致最终的估计量形式错误。考虑到学生完整展示了最大似然估计的求解过程，给2分。

（2）得分及理由（满分6分）

由于第一部分得到的估计量形式错误，导致方差计算的基础错误。此外，学生在方差计算中存在多处逻辑错误：

• 错误地将D(∑X_i+∑2Y_j)直接写成D(∑X_i)+D(∑2Y_j)
• 错误地计算了D(∑2Y_j)=4mD(Y_j)
• 最后一步D(ˆθ)的计算公式完全错误

考虑到学生尝试使用方差的性质进行计算，但核心逻辑存在严重错误，给1分。

题目总分：2+1=3分