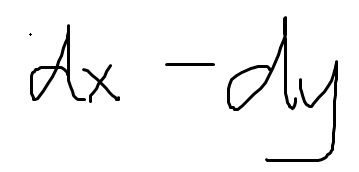
评分及理由

（1）得分及理由（满分5分）

学生作答识别结果为“$Ax - Ay$”。根据题目条件，函数$f(x,y)$可微，曲面与$xOy$坐标面的交线给出条件，且已知$f'_x(0,0)=1$。通过分析可知，交线在$xOy$平面上满足$z=0$，因此沿该交线有$f(x,y)=0$。对该式求导并结合已知条件可解得$f'_y(0,0)=-1$。于是全微分$\mathrm{d}z|_{(0,0)} = f'_x(0,0)\mathrm{d}x + f'_y(0,0)\mathrm{d}y = \mathrm{d}x - \mathrm{d}y$。

学生答案“$Ax - Ay$”中，若将“A”视为误写的“d”（微分符号），则形式与标准答案$\mathrm{d}x - \mathrm{d}y$一致。根据题目要求，对识别错误导致的相似字符误写不扣分。因此该答案在纠正误写后与标准答案等价。

得分为5分。

题目总分：5分