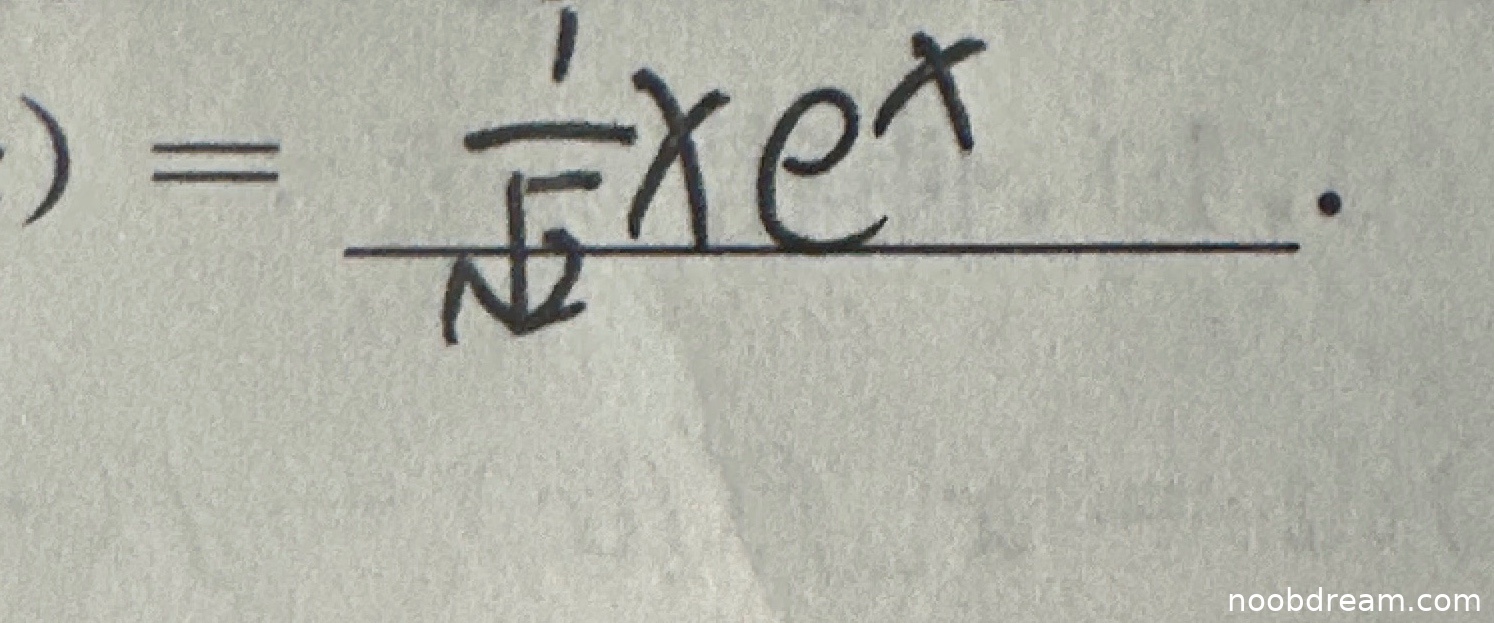
评分及理由

（1）得分及理由（满分5分）

学生给出的答案是 $\frac{1}{\sqrt{2}}xe^{x}$，而标准答案是 $-xe^x + 2x^2e^x$。

首先分析微分方程 $y''' - 3y'' + 3y' - y = 0$，其特征方程为 $r^3 - 3r^2 + 3r - 1 = 0$，即 $(r-1)^3 = 0$，因此通解为 $y(x) = (C_1 + C_2x + C_3x^2)e^x$。

题目给出在点 $(0,0)$ 的曲率圆为 $(x-1)^2 + (y-1)^2 = 2$，说明： - 曲线过点 $(0,0)$：代入得 $y(0)=0$ ⇒ $C_1=0$ - 曲率圆心为 $(1,1)$，半径为 $\sqrt{2}$ - 曲率公式 $k = \frac{|y''|}{(1+y'^2)^{3/2}}$，在 $x=0$ 时曲率半径 $R = \frac{1}{k} = \sqrt{2}$ - 圆心坐标与曲线关系：圆心在法线上，且距离切点 $R$

学生答案 $\frac{1}{\sqrt{2}}xe^x$ 形式为 $Axe^x$，这只能满足 $C_1=0$ 和过原点条件，但无法同时满足曲率圆给出的 $y'(0)$ 和 $y''(0)$ 的条件。具体来说： - $y'(0) = A$，$y''(0) = 2A$ - 曲率圆条件要求 $y'(0)=1$，$y''(0)=1$（通过计算曲率圆几何关系可得） - 但学生答案无法同时满足这两个条件

因此，学生的答案与标准答案完全不同，且不满足题目给出的曲率圆条件，属于逻辑错误。

得分：0分

题目总分：0分