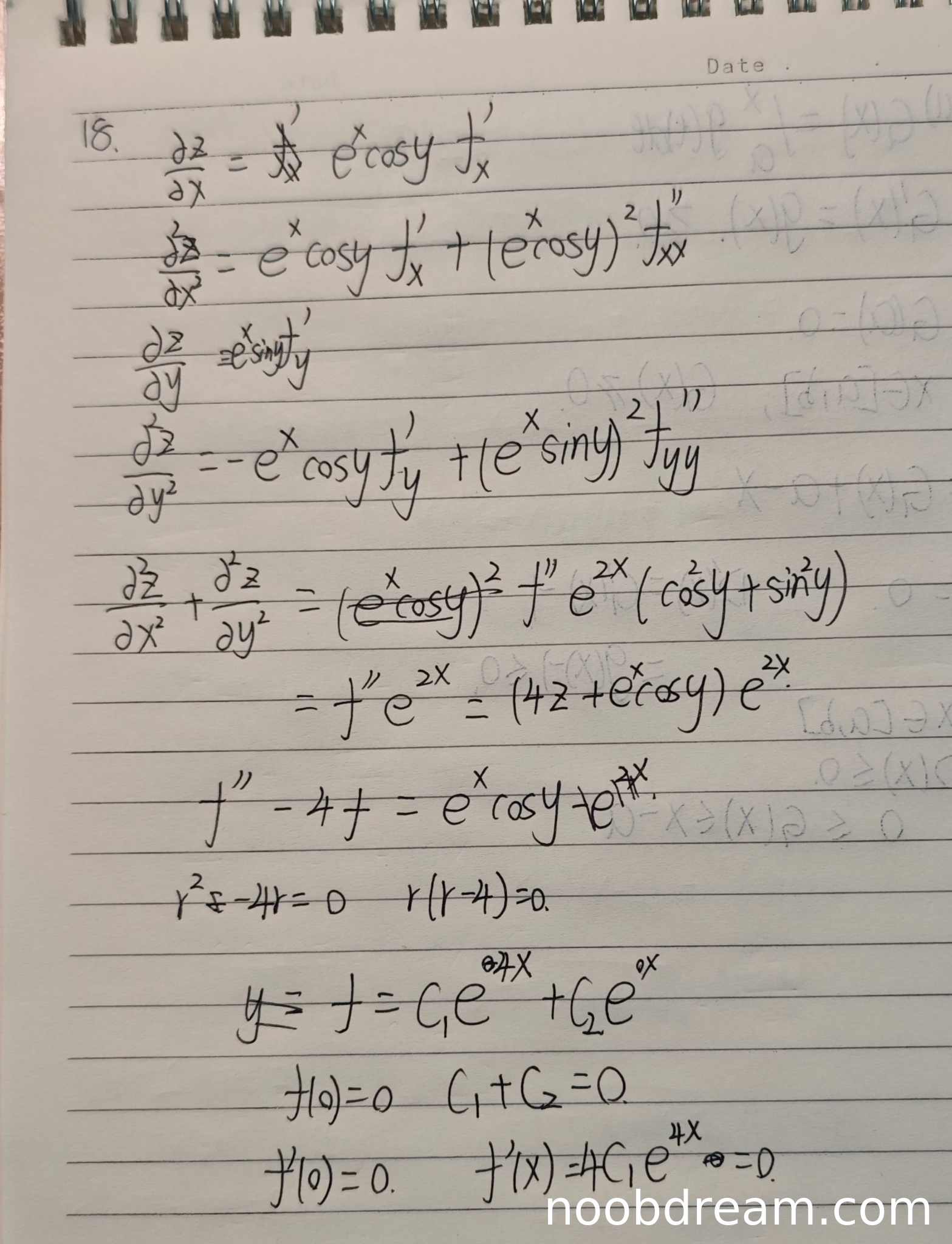
评分及理由

（1）偏导数计算部分（满分3分）

学生正确计算了一阶偏导数：∂z/∂x = e^x cos y f'，∂z/∂y = -e^x sin y f'。二阶偏导数计算基本正确：∂²z/∂x² = e^x cos y f' + e^(2x)cos²y f''，∂²z/∂y² = -e^x cos y f' + e^(2x)sin²y f''。在求和时正确得到∂²z/∂x² + ∂²z/∂y² = e^(2x)f''。这部分计算完整正确，得3分。

（2）建立微分方程部分（满分2分）

学生将拉普拉斯算子结果代入给定方程，得到f''e^(2x) = (4z + e^x cos y)e^(2x)，然后化简为f'' - 4f = e^x cos y。这里存在逻辑错误：方程右边应该是关于u = e^x cos y的函数，但学生保留了e^x cos y，没有替换为u。这导致后续求解错误。扣1分，得1分。

（3）微分方程求解部分（满分3分）

学生求解f'' - 4f = e^x cos y时，特征方程计算错误：应该是r² - 4 = 0，但学生写成了r² - 4r = 0。齐次解应为C₁e^(2u) + C₂e^(-2u)，但学生得到C₁e^(4x) + C₂。非齐次方程特解部分完全缺失。这部分存在严重逻辑错误，扣2分，得1分。

（4）初始条件应用部分（满分2分）

学生虽然写出了初始条件f(0)=0，f'(0)=0，但由于前面方程错误，得到的解f(x)=0显然不正确。这部分得0分。

题目总分：3+1+1+0=5分