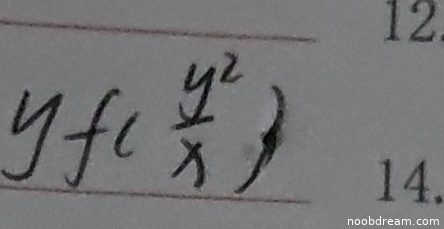
评分及理由

（1）得分及理由（满分4分）

学生两次识别结果均为：$yf(\frac{y^{2}}{x})$，这与标准答案 $y f\left(\frac{y^{2}}{x}\right)$ 完全一致。

根据题目要求，函数 $f(u)$ 可导，$z=y f(\frac{y^{2}}{x})$，需要计算 $2 x \frac{\partial z}{\partial x}+y \frac{\partial z}{\partial y}$。

计算过程为：

设 $u = \frac{y^2}{x}$，则 $z = y f(u)$

$\frac{\partial z}{\partial x} = y f'(u) \cdot (-\frac{y^2}{x^2}) = -\frac{y^3}{x^2} f'(u)$

$\frac{\partial z}{\partial y} = f(u) + y f'(u) \cdot \frac{2y}{x} = f(u) + \frac{2y^2}{x} f'(u)$

代入表达式：

$2x \frac{\partial z}{\partial x} + y \frac{\partial z}{\partial y} = 2x \cdot (-\frac{y^3}{x^2} f'(u)) + y \cdot (f(u) + \frac{2y^2}{x} f'(u))$

$= -\frac{2y^3}{x} f'(u) + y f(u) + \frac{2y^3}{x} f'(u) = y f(u) = y f(\frac{y^2}{x})$

学生答案与正确结果一致，因此得4分。

题目总分：4分