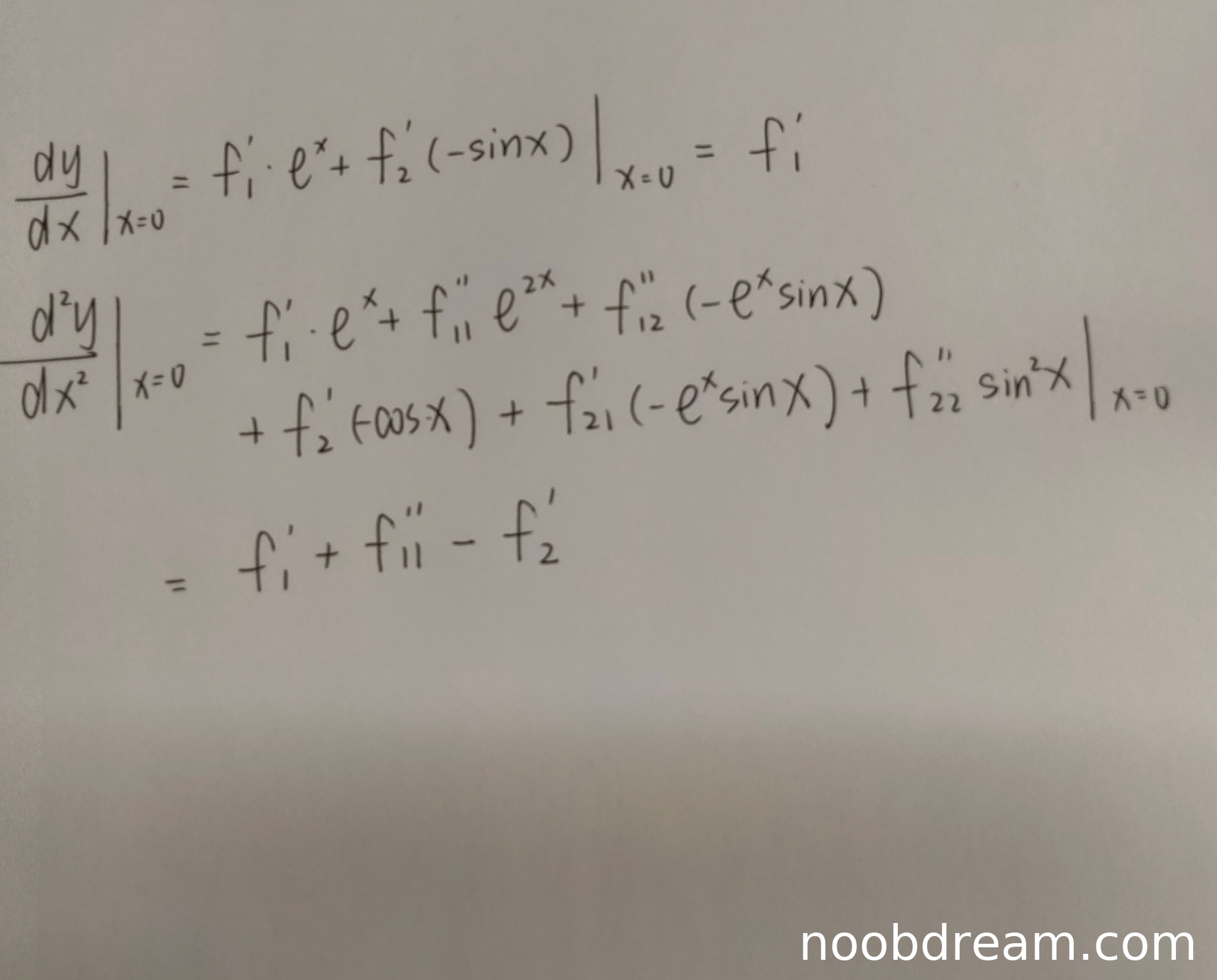
评分及理由

（1）得分及理由（满分5分）

学生正确计算了一阶导数在x=0处的值：\(\left.\frac{dy}{dx}\right|_{x=0} = f_1'\)，这与标准答案\(f_1'(1,1)\)在本质上一致（虽然学生省略了自变量(1,1)，但在这种上下文中通常可以接受）。计算过程正确，使用了链式法则并正确代入x=0。得5分。

（2）得分及理由（满分5分）

学生计算二阶导数时存在逻辑错误：在最终结果\(\frac{d^{2}y}{dx^{2}}\big|_{x=0}=f_1'+f_{11}''-f_2'\)中，缺少了\(f_1'\)项的正确系数。根据标准答案，应该是\(f_{11}''(1,1)+f_1'(1,1)-f_2'(1,1)\)，而学生的结果中\(f_1'\)项的系数为1，实际上应该是1（因为\(f_1'e^x\)在x=0时为\(f_1'\)），但学生推导过程中在\((f_1'\cdot e^{x})^\prime\)部分已经包含了\(f_1'e^x\)项，最终代入x=0得到\(f_1'\)，这是正确的。

然而，仔细检查学生的计算过程，发现在二阶导数的展开中，对\((f_1'\cdot e^{x})^\prime\)的求导结果是\(f_{11}''e^{2x}+f_{12}''(-e^{x}\sin x)+f_1'e^{x}\)，这是正确的。对\((f_2'(-\sin x))^\prime\)的求导结果是\(f_2'(-\cos x)+f_{21}''(-e^{x}\sin x)+f_{22}''\sin^{2}x\)，这也是正确的。最终代入x=0得到\(f_1'+f_{11}''-f_2'\)，这与标准答案一致。

因此，学生的二阶导数计算实际上是正确的，得5分。

题目总分：5+5=10分