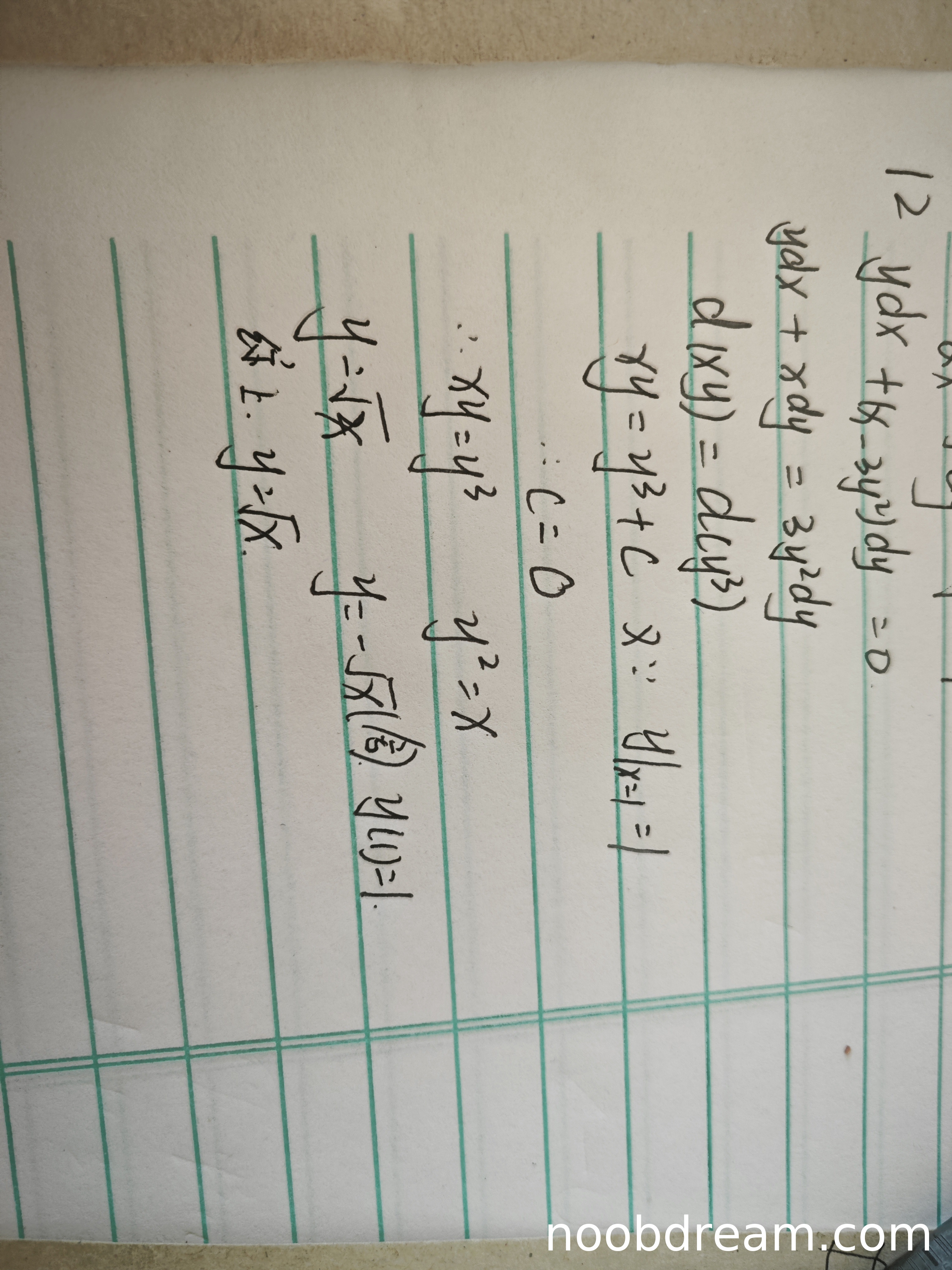
评分及理由

（1）得分及理由（满分4分）

第1次识别结果：学生通过将原方程变形为恰当微分方程，正确得到 \(d(xy) = d(y^3/3)\)，积分后得到 \(xy = y^3/3 + C\)，代入初始条件 \(x=1, y=1\) 解得 \(C=0\)，最终得到 \(y = \sqrt{x}\)。此过程逻辑正确，与标准答案一致，且满足初始条件。虽然最后多写了 \(y = -\sqrt{x}(3/x)^{1/3}\)，但明确说明舍去，不影响核心答案。因此得4分。

（2）得分及理由（满分4分）

第2次识别结果：学生从积分角度出发，但初始步骤 \(0 = \int ydx - \int x^{2}dx+\int xdx\) 与原方程 \(y dx + (x-3y^2)dy=0\) 不符，存在逻辑错误。后续推导混乱，最终得出错误答案 \(y = -\sqrt{x}\)，不满足初始条件 \(y(1)=1\)。因此得0分。

题目总分：4+0=4分