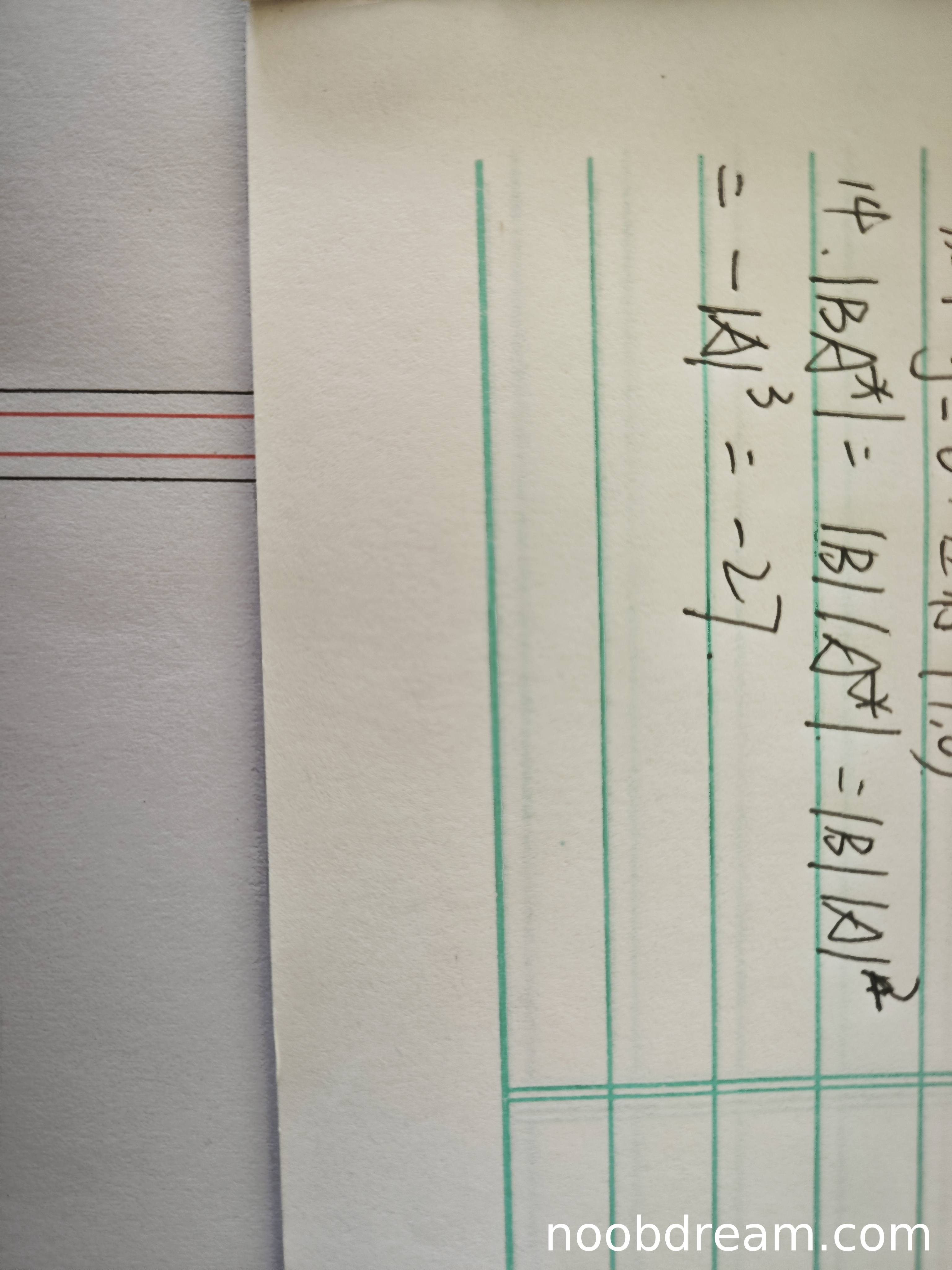
评分及理由

（1）得分及理由（满分4分）

学生作答给出了两个识别结果。第一次识别结果：

• 步骤1：\(|BA^{*}| = |B||A^{*}|\) 正确（行列式乘积性质）
• 步骤2：\(|B||A^{*}| = |B||A|^{2}\) 正确（伴随矩阵行列式公式 \(|A^{*}| = |A|^{n-1}\)，这里 \(n=3\)）
• 步骤3：\(|B||A|^{2} = -|A|^{3}\) 正确（交换两行行列式变号，所以 \(|B| = -|A|\)，代入得 \(-|A| \cdot |A|^2 = -|A|^3\)）
• 步骤4：\(-|A|^{3} = -27\) 正确（已知 \(|A|=3\)）

第二次识别结果：

• 步骤1：\(|BA^{*}| = |B||A^{*}|\) 正确
• 步骤2：\(|B||A^{*}| = |B||A|^{n-1}\) 正确（一般公式）
• 步骤3：\(=-|A|^{3}\) 正确（代入 \(n=3\) 和 \(|B| = -|A|\)）
• 步骤4：\(=-27\) 正确

两个识别结果的核心逻辑完全正确，最终答案都是 \(-27\)，与标准答案一致。根据评分要求，只要有一次识别正确就不扣分，且思路正确、计算正确。

得分：4分

题目总分：4分