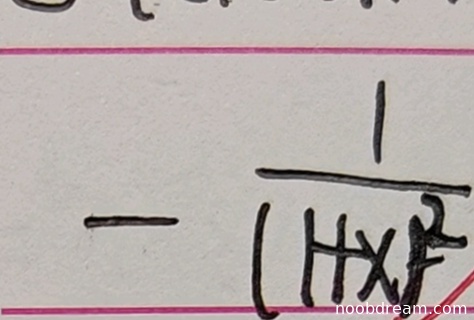
评分及理由

（1）得分及理由（满分4分）

学生两次识别结果均为：$-\frac{1}{(1 + x)^{2}}$，而标准答案为$\frac{1}{(1+x)^2}$。两者符号相反。

幂级数$\sum_{n=1}^{\infty} (-1)^{n-1}nx^{n-1}$在区间$(-1,1)$内的和函数推导过程如下：

设$S(x) = \sum_{n=1}^{\infty} (-1)^{n-1}nx^{n-1}$

考虑几何级数$\sum_{n=1}^{\infty} (-1)^{n-1}x^{n} = \frac{x}{1+x}$，其中$|x|<1$

对两边求导：$\frac{d}{dx}\left[\frac{x}{1+x}\right] = \sum_{n=1}^{\infty} (-1)^{n-1}nx^{n-1}$

计算导数：$\frac{d}{dx}\left[\frac{x}{1+x}\right] = \frac{(1+x)-x}{(1+x)^2} = \frac{1}{(1+x)^2}$

因此，正确的和函数应为$\frac{1}{(1+x)^2}$，学生答案多了一个负号，这是一个逻辑错误。

根据评分规则，存在逻辑错误不能给满分，因此本题得0分。

题目总分：0分