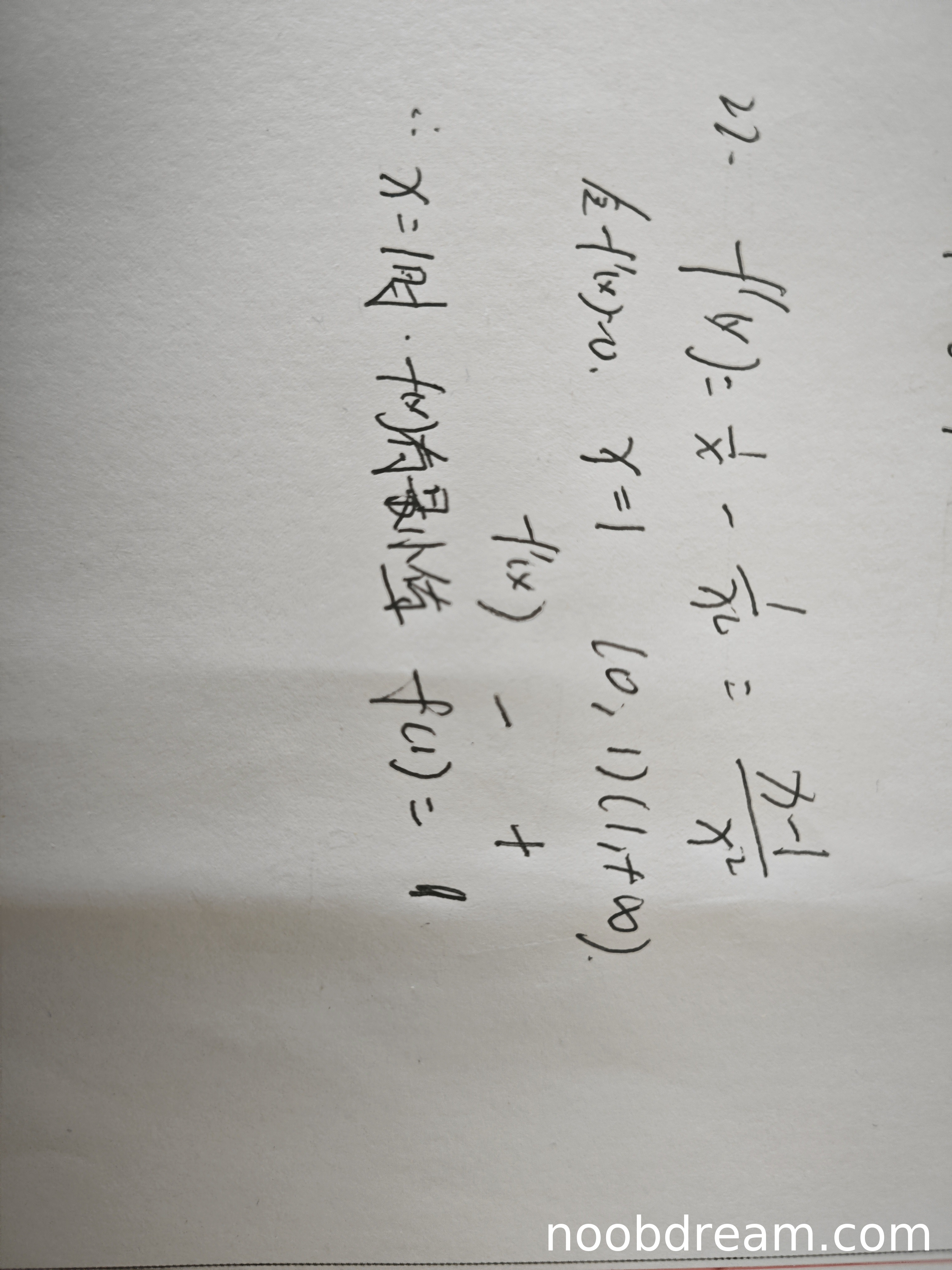
评分及理由

（1）得分及理由（满分5分）

学生作答中，第一次识别结果正确求出了导数 \( f'(x) = \frac{1}{x} - \frac{1}{x^2} = \frac{x-1}{x^2} \)，并正确分析了单调区间：在 (0,1) 上 \( f'(x) < 0 \)（单调递减），在 (1,+∞) 上 \( f'(x) > 0 \)（单调递增），从而得出在 \( x=1 \) 处取得最小值。但计算最小值时，第一次识别结果为 \( f(1) = 0 \)，而正确值应为 \( f(1) = \ln 1 + \frac{1}{1} = 1 \)。第二次识别结果中，函数表达式错误写为 \( f(x) = x - \frac{1}{x} \)，与题目所给 \( f(x) = \ln x + \frac{1}{x} \) 不符，导致后续分析全部错误。由于两次识别结果中至少有一次（第一次）在导数、单调性和极值点分析上正确，但最小值计算错误，且第二次识别因函数表达式错误导致逻辑错误，因此扣分。具体扣分：导数与单调性分析正确（3分），最小值计算错误（扣2分），得3分。

（2）得分及理由（满分6分）

学生作答中未对第(2)问进行任何解答，因此本题得0分。

题目总分：3+0=3分