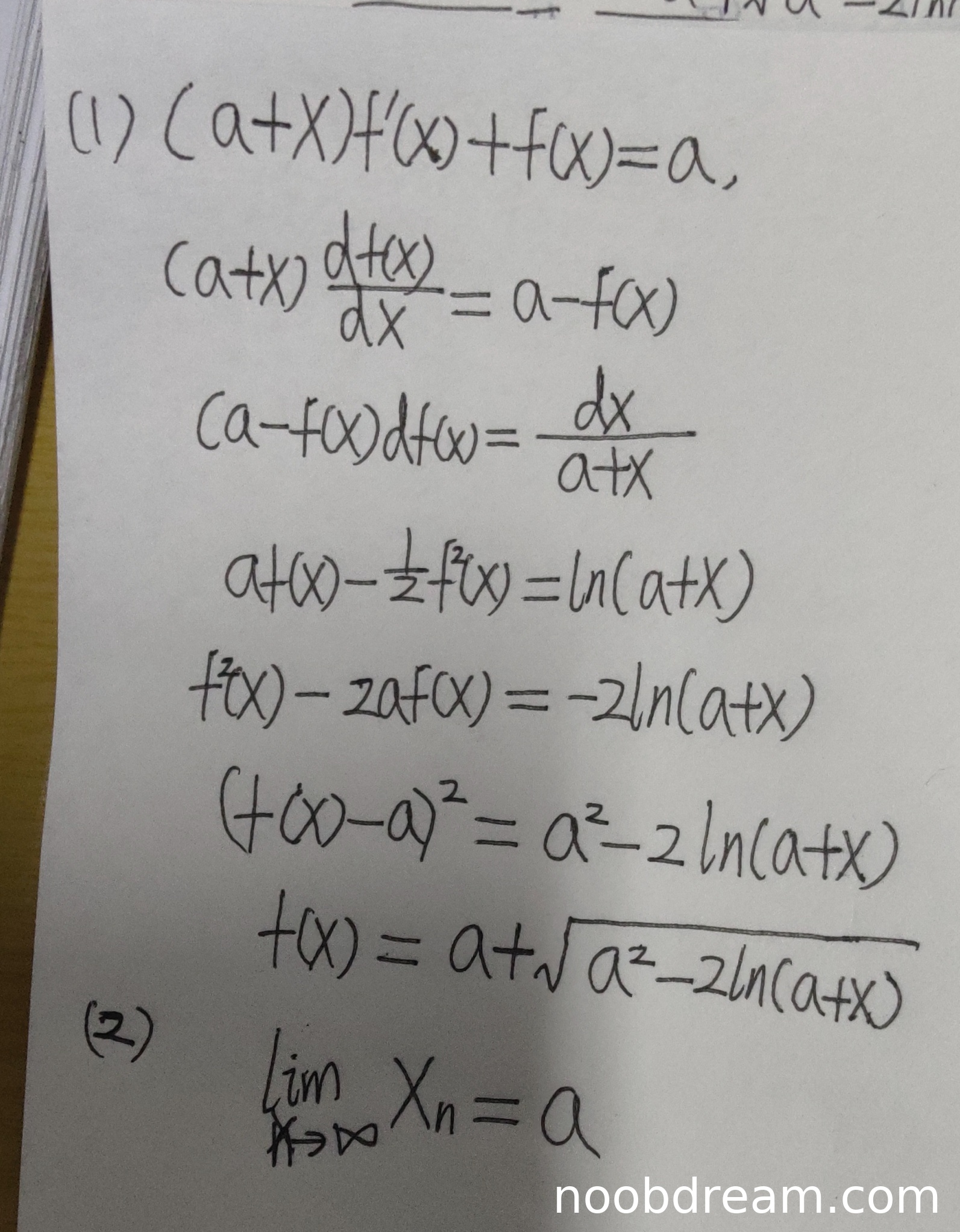
评分及理由

（1）得分及理由（满分6分）

学生解答第（Ⅰ）问时，将微分方程 $(a+x)f'(x)+f(x)=a$ 变形为 $(a+x)\frac{df(x)}{dx}=a-f(x)$ 后，错误地分离变量为 $(a-f(x))df(x)=\frac{dx}{a+x}$，这是逻辑错误，因为正确的分离变量应为 $\frac{df(x)}{a-f(x)} = \frac{dx}{a+x}$。后续的积分步骤 $af(x)-\frac12 f^2(x)=\ln(a+x)$ 等均基于此错误，导致最终结果 $f(x)=a+\sqrt{a^2-2\ln(a+x)}$ 不正确，且未利用初始条件 $f(0)=1$ 确定常数。因此，第（Ⅰ）问得0分。

（2）得分及理由（满分6分）

学生解答第（Ⅱ）问时，直接给出 $\lim_{n\to\infty}x_n=a$，但未提供任何证明过程。标准答案中需分 $a>1$ 和 $\frac12\leq a<1$ 两种情况讨论序列的单调性、有界性及极限值，并最终得出 $\lim_{n\to\infty}x_n=\sqrt{a}$。学生答案与正确结果不符，且无合理推导，因此第（Ⅱ）问得0分。

题目总分：0+0=0分