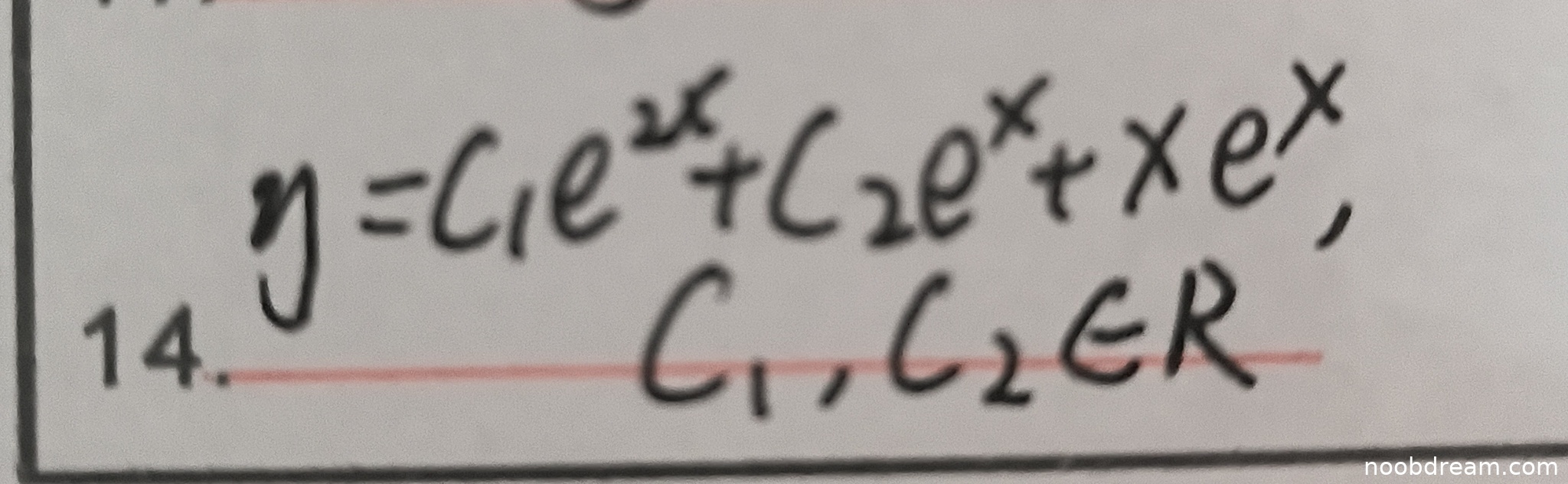
评分及理由

（1）得分及理由（满分5分）

学生作答的两次识别结果均为：\( y = C_1 e^{2x} + C_2 e^x + x e^x \)，其中 \( C_1, C_2 \in \mathbb{R} \)。标准答案为：\( y = C_1 e^x + C_2 e^{2x} + x e^x \)。

对比发现，学生答案中 \( e^x \) 和 \( e^{2x} \) 对应的任意常数 \( C_1, C_2 \) 的顺序与标准答案相反。但在微分方程的通解中，齐次解部分的两个线性无关解 \( e^x \) 和 \( e^{2x} \) 的顺序不影响通解的正确性，因为 \( C_1, C_2 \) 是任意常数，可以互换。因此，学生的答案与标准答案本质相同，只是符号表示顺序不同，这属于等价形式。

根据评分要求，思路正确不扣分，且由于字符识别可能存在的顺序问题不影响核心逻辑，故不扣分。

得分：5分

题目总分：5分