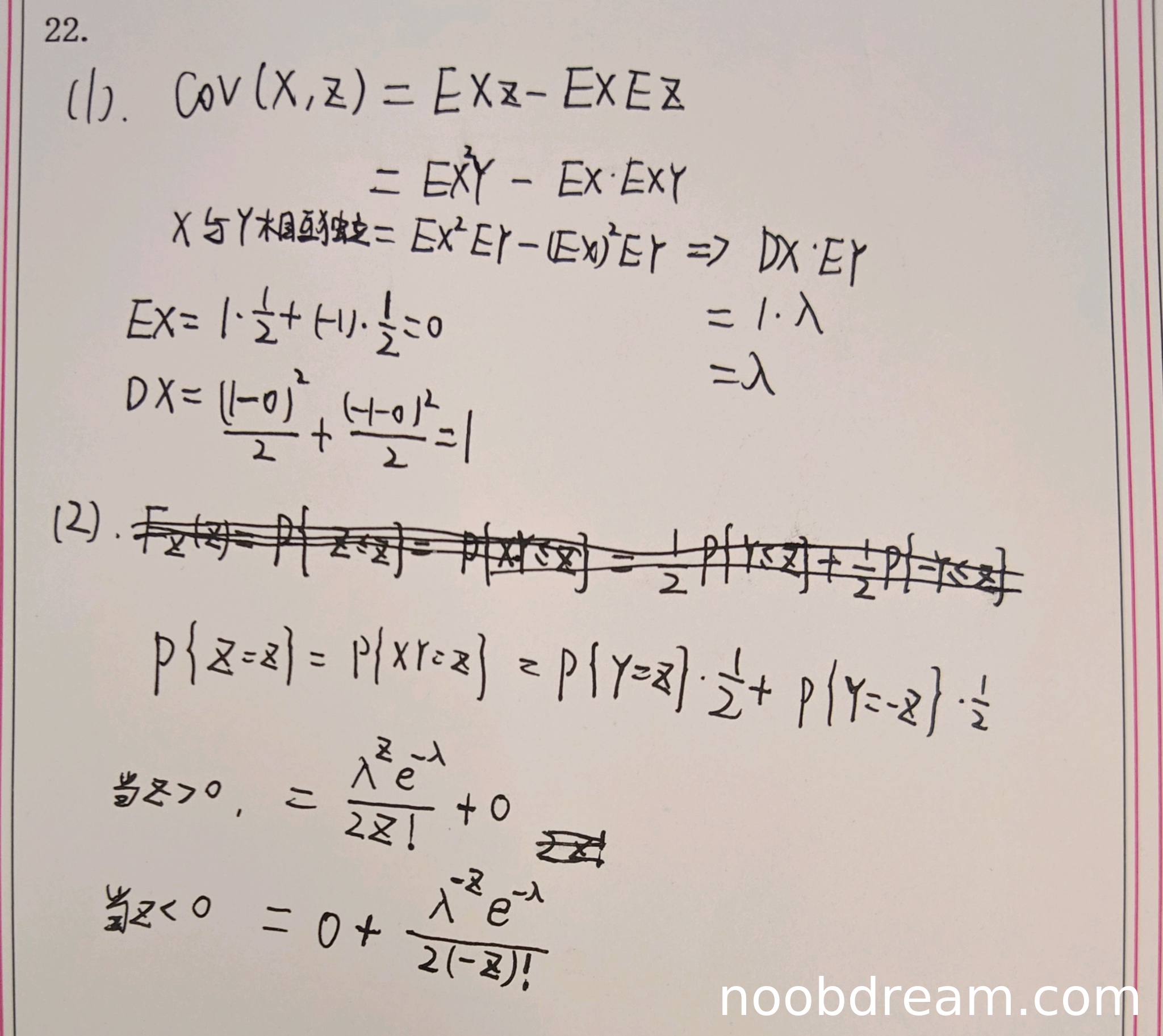
评分及理由

（1）得分及理由（满分5.5分）

学生作答中，第1次识别结果在计算Cov(X,Z)时，第一步写成了EX^3Y，这是明显的逻辑错误（应为EX^2Y），但后续计算中实际使用了EX^2Y，可能是识别错误。第2次识别结果正确使用了公式Cov(X,Z)=E(XZ)-E(X)E(Z)，并正确推导出E(X^2Y)-E(X)E(XY)，利用独立性得到E(X^2)E(Y)-(E(X))^2E(Y)=D(X)E(Y)，计算E(X)=0、D(X)=1、E(Y)=λ，最终结果λ正确。虽然第1次识别有误写，但第2次识别完全正确，根据规则“只要其中有一次回答正确则不扣分”，且误写不扣分，因此本小题得满分5.5分。

（2）得分及理由（满分5.5分）

学生作答中，第1次识别结果将Z=XY误写为X+Y，导致整个概率分布计算错误，这是严重的逻辑错误。第2次识别结果正确写出Z=XY，并给出F_Z(z)=P{XY≤z}的分解，但在计算概率质量函数时，错误地写成P{Z=z}=P{Y=z}·1/2+P{Y=-z}·1/2，这忽略了X和Y的取值关系（例如当z>0时，只能由X=1,Y=z得到，不能由X=-1,Y=-z得到，因为Y≥0）。具体错误包括：当z>0时，学生结果中多加了0项，但表达式λ^{z}e^{-λ}/(2z!)正确；当z<0时，学生结果λ^{-z}e^{-λ}/(2(-z)!)正确；但缺失了k=0的情况，且未区分Y的取值范围（Y≥0）。标准答案中k=0时概率为e^{-λ}，学生完全遗漏。由于存在根本性的逻辑错误（错误理解Z=XY的取值情况），扣5分，本小题得0.5分。

题目总分：5.5+0.5=6分