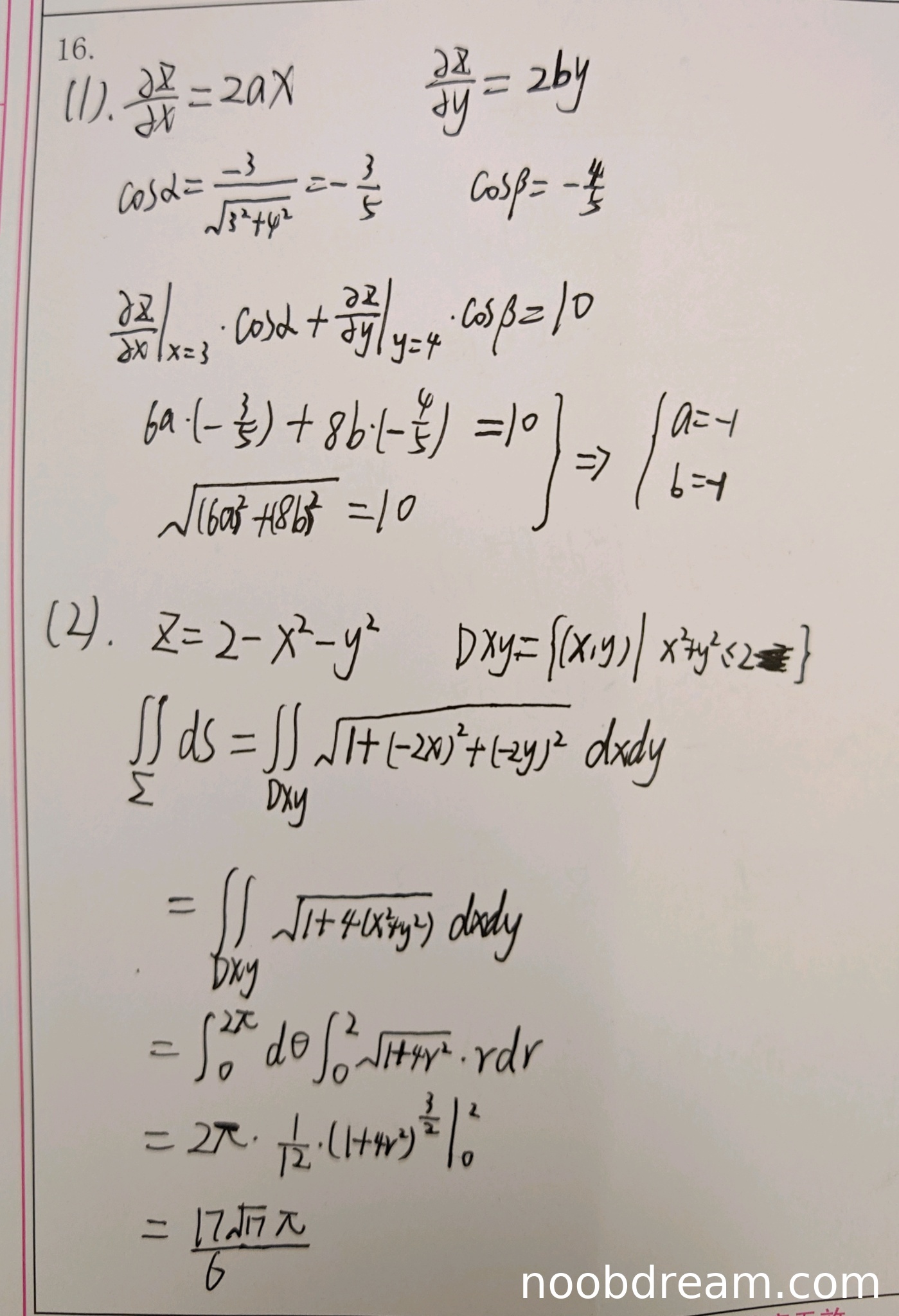
评分及理由

（Ⅰ）得分及理由（满分5分）

学生作答中，第一次识别结果和第二次识别结果都正确求出了a = -1, b = -1。

第一次识别：使用了方向导数公式和梯度模长两个条件建立方程组，思路正确，计算无误。

第二次识别：同样使用了方向导数公式和梯度模长两个条件，虽然计算过程略有不同，但最终结果正确。

两种识别结果都得到了正确答案，因此给满分5分。

（Ⅱ）得分及理由（满分5分）

学生作答中，两次识别结果都正确建立了曲面积分表达式，使用了极坐标变换，但在积分上限和计算上存在错误。

正确积分区域应为：0 ≤ r ≤ √2

正确积分表达式：∫₀²π dθ ∫₀^√2 √(1+4r²) r dr

但学生计算时：

第一次识别：积分上限写成了2（应为√2），计算结果是(17√17π)/6

第二次识别：积分上限写成了√2，但计算过程中积分限代入时仍按r=2计算，得到(17√17π)/6

正确结果应为：当r=√2时，1+4r² = 1+8 = 9，积分结果应为(π/6)(27-1) = (13π)/3

由于积分上限错误导致最终结果错误，扣2分。

得分：5-2 = 3分

题目总分：5+3=8分