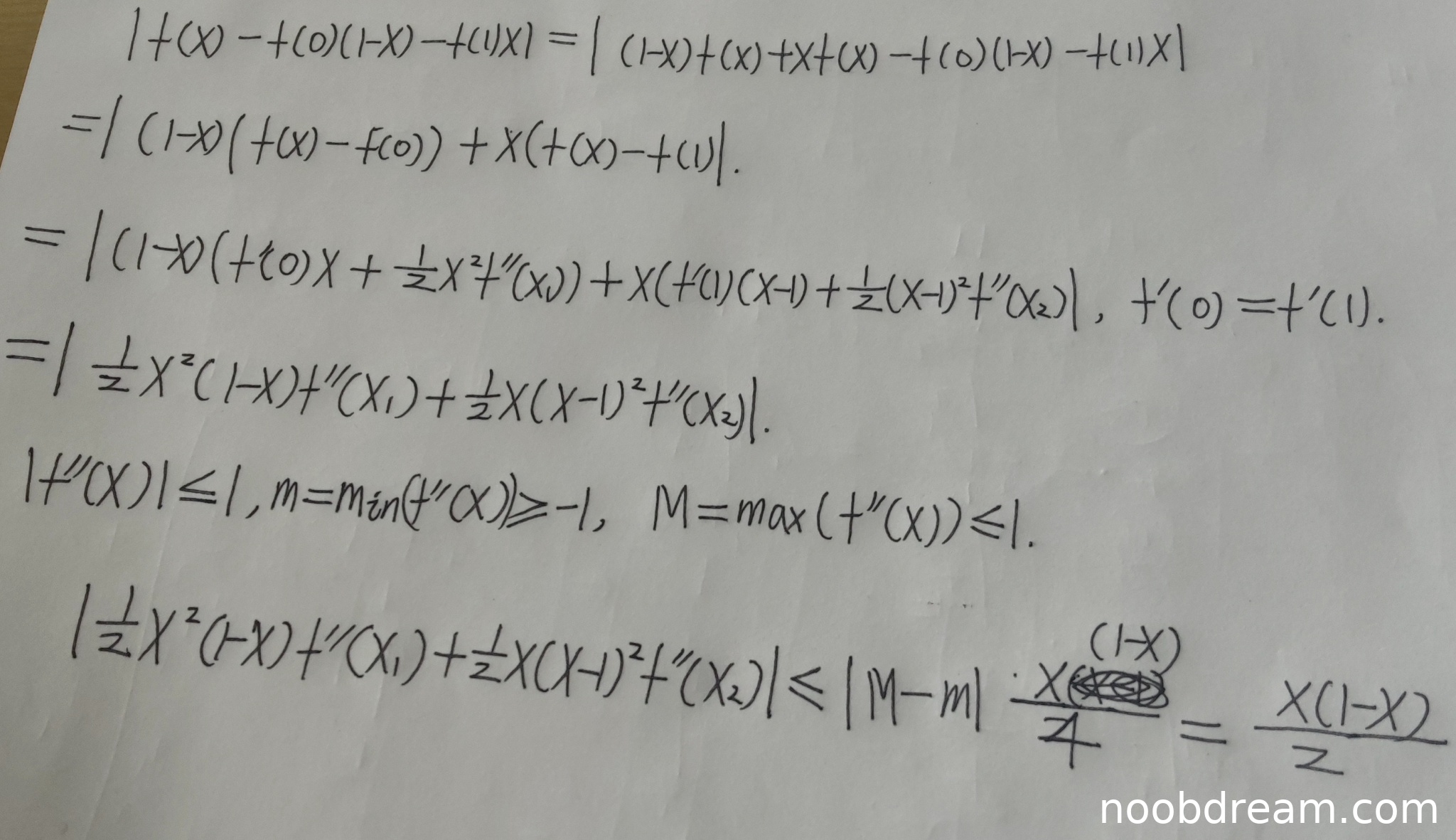
评分及理由

（1）得分及理由（满分6分）

学生使用了泰勒展开的方法来证明不等式，思路与标准答案不同但正确。具体步骤：

• 正确写出表达式 \(f(x)-f(0)(1-x)-f(1)x\) 并展开
• 利用泰勒公式 \(f(x)=f(0)+f'(0)x+\frac{1}{2}x^2f''(x_1)\) 和 \(f(x)=f(1)+f'(1)(x-1)+\frac{1}{2}(x-1)^2f''(x_2)\)
• 正确应用条件 \(f'(0)=f'(1)\) 消去一阶导数项
• 得到 \(\left|\frac{1}{2}x^2(1-x)f''(x_1)+\frac{1}{2}x(x-1)^2f''(x_2)\right|\)
• 利用 \(|f''(x)|\leq 1\) 进行放缩

但最后一步放缩存在问题：学生写的是 \(\leq |M-m|\frac{x(1-x)}{2}\)，实际上应该是 \(\leq \frac{x(1-x)}{2}\)，因为 \(|f''(x_1)|,|f''(x_2)|\leq 1\)，所以直接有 \(\left|\frac{1}{2}x^2(1-x)f''(x_1)+\frac{1}{2}x(x-1)^2f''(x_2)\right| \leq \frac{1}{2}x^2(1-x)+\frac{1}{2}x(1-x)^2 = \frac{x(1-x)}{2}\)。

学生引入 \(M,m\) 的概念但使用不当，这是逻辑错误。由于思路基本正确，主要步骤完整，扣1分。

得分：5分

（2）得分及理由（满分6分）

学生没有给出第(2)问的解答。根据题目要求，只对给出的部分进行评分。

得分：0分

题目总分：5+0=5分