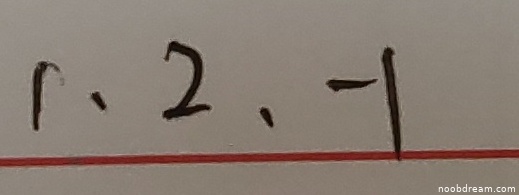
评分及理由

（1）得分及理由（满分5分）

学生给出的答案是“1, 2, -1”，而标准答案是“0, 1, 1”。

分析：矩阵 \( A \) 是 \( 3 \times 2 \) 矩阵，\( B \) 是 \( 2 \times 3 \) 矩阵，已知 \( BA = E \)（其中 \( E \) 是 \( 2 \times 2 \) 单位矩阵）。那么 \( AB \) 是一个 \( 3 \times 3 \) 矩阵。由于 \( BA = E \)，说明 \( B \) 是 \( A \) 的左逆，因此 \( A \) 列满秩（秩为 2），\( B \) 行满秩（秩为 2）。

考虑 \( (AB)^2 = A(BA)B = AEB = AB \)，所以 \( AB \) 是幂等矩阵，其特征值只能是 0 或 1。又因为 \( \operatorname{rank}(AB) = \operatorname{rank}(A) = 2 \)，所以 \( AB \) 的非零特征值个数为 2，零特征值个数为 1，即特征值为 0, 1, 1。

学生答案“1, 2, -1”中出现了 2 和 -1，这不符合幂等矩阵特征值的性质，属于逻辑错误，因此答案错误。

得分：0 分。

题目总分：0 分