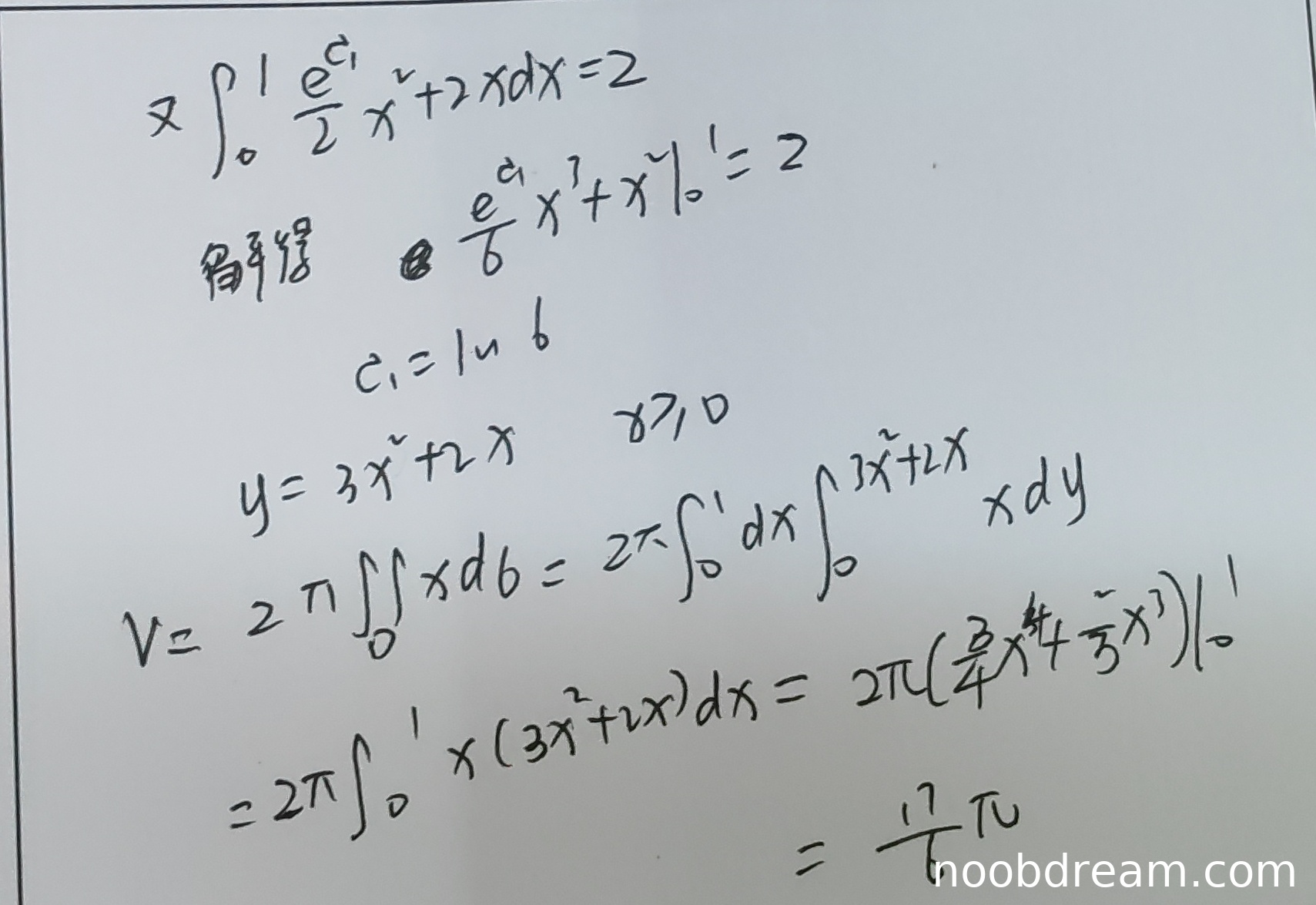
评分及理由

（1）微分方程求解部分（满分4分）

学生正确设 \( y' = p \)，代入原方程得到 \( xp' - p + 2 = 0 \)，并分离变量得到 \( \frac{dp}{p-2} = \frac{1}{x}dx \)。积分得到 \( \ln|p-2| = \ln|x| + c_1 \)，进而得到 \( p = e^{c_1}x + 2 \)。再积分得到 \( y = \frac{e^{c_1}}{2}x^2 + 2x + c_2 \)，利用 \( y(0) = 0 \) 得到 \( c_2 = 0 \)。此部分思路正确，计算无误，得4分。

（2）利用面积条件确定常数部分（满分3分）

学生正确写出面积条件 \( \int_0^1 \left( \frac{e^{c_1}}{2}x^2 + 2x \right) dx = 2 \)，并正确计算积分得到 \( \frac{e^{c_1}}{6} + 1 = 2 \)，解得 \( e^{c_1} = 6 \)，即 \( c_1 = \ln 6 \)，从而得到 \( y = 3x^2 + 2x \)。此部分思路正确，计算无误，得3分。

（3）旋转体体积计算部分（满分3分）

学生正确使用旋转体体积公式 \( V = 2\pi \iint x d\sigma = 2\pi \int_0^1 dx \int_0^{3x^2+2x} x dy \)，正确计算内层积分得到 \( x(3x^2+2x) \)，然后计算 \( 2\pi \int_0^1 (3x^3+2x^2) dx \)，最终得到 \( \frac{17\pi}{6} \)。此部分思路正确，计算无误，得3分。

题目总分：4+3+3=10分