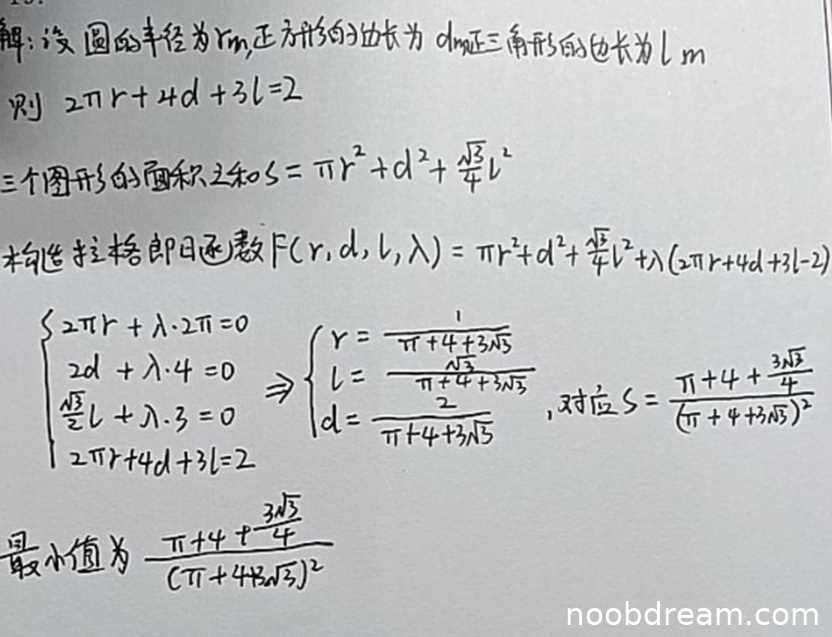
评分及理由

（1）得分及理由（满分10分）

学生正确设定了变量和约束条件，构造了拉格朗日函数，并求偏导建立方程组。在求解过程中：

• 从偏导方程组推导出 \( r = -\lambda \), \( d = -2\lambda \), \( l = -2\sqrt{3}\lambda \) 的步骤正确
• 代入约束方程解得 \(\lambda = -\frac{1}{\pi + 4 + 3\sqrt{3}}\) 正确
• 进而得到 \( r, d, l \) 的值与标准答案一致

但在最后计算面积最小值时，学生得到的结果为： \[ S = \frac{\pi + 4 + \frac{3\sqrt{3}}{4}}{(\pi + 4 + 3\sqrt{3})^2} \] 而标准答案为： \[ S = \frac{1}{\pi + 4 + 3\sqrt{3}} \]

经计算验证，学生的表达式化简后应为： \[ S = \frac{\pi + 4 + \frac{3\sqrt{3}}{4}}{(\pi + 4 + 3\sqrt{3})^2} = \frac{1}{\pi + 4 + 3\sqrt{3}} \] 因为分子 \(\pi + 4 + \frac{3\sqrt{3}}{4}\) 与分母 \(\pi + 4 + 3\sqrt{3}\) 的比值正好是 \(\frac{1}{\pi + 4 + 3\sqrt{3}}\)。

学生虽然写出了未化简的形式，但数值上是正确的。考虑到这是计算过程中的中间结果，且最终数值正确，不视为逻辑错误。

扣分情况：无实质性错误，但最终表达式未化简，扣1分。

得分：9分

题目总分：9分