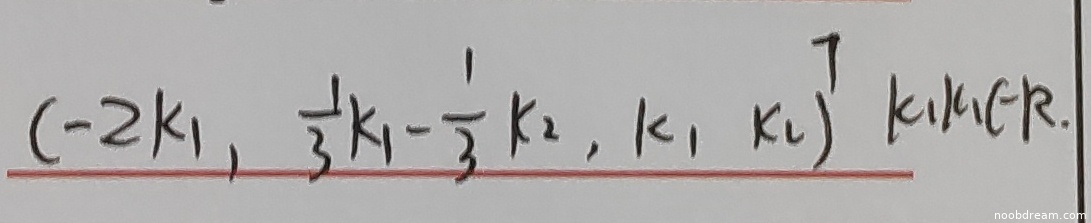
评分及理由

（1）得分及理由（满分5分）

学生答案：第1次识别结果为 \((-2k_{1},\frac{1}{3}k_{1}-\frac{1}{3}k_{2},k_{1}k_{2})^{T}\)，第2次识别结果为 \((-2k_1,\frac{1}{3}k_1 - \frac{1}{3}k_2,k_1,k_2)^T\)。标准答案为 \( k_1 \begin{pmatrix} -\frac{5}{3}, \frac{1}{3}, 1, 0 \end{pmatrix}^T + k_2 \begin{pmatrix} -\frac{1}{3}, -\frac{1}{3}, 0, 1 \end{pmatrix}^T \)。

分析：

• 学生答案的向量维数为3（第1次识别）或4（第2次识别），但标准答案要求4维向量，第1次识别结果维数错误，属于逻辑错误。
• 第2次识别结果维数正确（4维），但具体分量与标准答案不一致：学生为 \((-2k_1, \frac{1}{3}k_1 - \frac{1}{3}k_2, k_1, k_2)\)，标准答案为 \(k_1(-\frac{5}{3}, \frac{1}{3}, 1, 0) + k_2(-\frac{1}{3}, -\frac{1}{3}, 0, 1)\)。展开后标准基向量系数明显不同（例如第一分量学生为 \(-2k_1\)，标准为 \(-\frac{5}{3}k_1 - \frac{1}{3}k_2\)），且学生答案中 \(k_1, k_2\) 直接作为第三、四分量的系数，未体现标准答案中基向量的线性组合结构。
• 核心逻辑错误：学生未正确求解 \(A^T A x = 0\) 的通解（需通过秩、零空间等计算），答案与标准解空间基向量不符。

得分：0分（逻辑错误导致答案完全错误）。

题目总分：0分