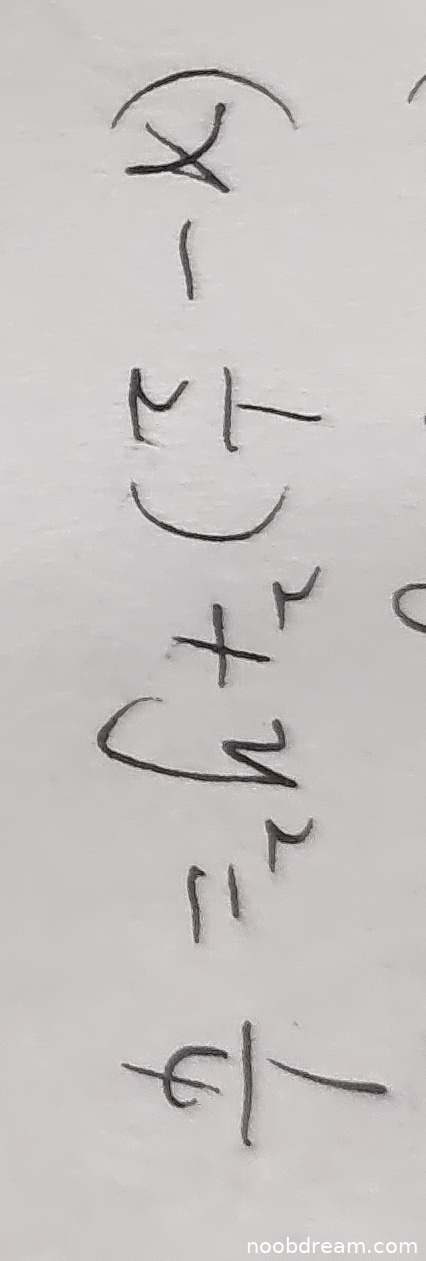
评分及理由

（1）得分及理由（满分5分）

学生作答为：$x - 1 + (y - 1)^2 = 1$，整理后为 $(y-1)^2 = 2 - x$。标准答案为 $(x-\frac{1}{2})^{2}+y^{2}=\frac{1}{4}$，表示圆心在 $(\frac{1}{2}, 0)$、半径为 $\frac{1}{2}$ 的圆。学生答案的圆心在 $(1,1)$、半径需要通过计算确定，与标准答案完全不同。

计算曲线 $y^2 = x$ 在点 $(0,0)$ 处的曲率：
一阶导数 $y' = \frac{1}{2y}$ 在 $(0,0)$ 处不存在，说明该点处切线垂直。使用参数方程 $x=t^2, y=t$，则 $\dot{x}=2t, \dot{y}=1, \ddot{x}=2, \ddot{y}=0$。
曲率公式 $k=\frac{|\dot{x}\ddot{y}-\dot{y}\ddot{x}|}{(\dot{x}^2+\dot{y}^2)^{3/2}} = \frac{|0-2|}{(4t^2+1)^{3/2}}$，在 $t=0$ 时 $k=2$。
曲率半径 $R=\frac{1}{k}=\frac{1}{2}$，曲率圆心在法线方向。在 $(0,0)$ 处法线为水平方向，圆心在 $(\frac{1}{2}, 0)$。

学生答案的圆心和半径都错误，说明计算过程存在根本性逻辑错误。根据评分规则，答案错误得0分。

题目总分：0分