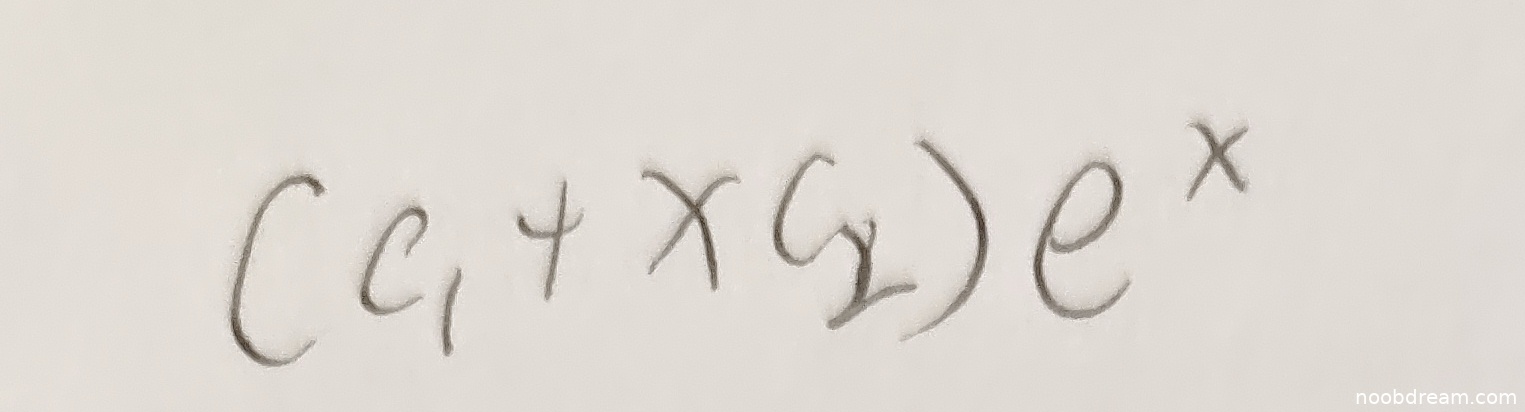
评分及理由

（1）得分及理由（满分5分）

学生给出的答案是$(c_{1}+xc_{2})e^{x}$，这是一个二阶线性微分方程的解的形式。然而，原方程是三阶微分方程$y^{\prime \prime \prime}-y=0$，其特征方程为$r^3-1=0$，解得特征根为$r=1$（三重根）。因此，通解应为$y=c_{1}e^{x}+c_{2}xe^{x}+c_{3}x^{2}e^{x}$。学生的答案缺少了$x^{2}e^{x}$项，仅包含两个任意常数，而三阶微分方程的通解应包含三个任意常数。这是一个逻辑错误，因为解的形式不完整，无法满足三阶方程的通解要求。因此，本题得0分。

题目总分：0分