评分及理由

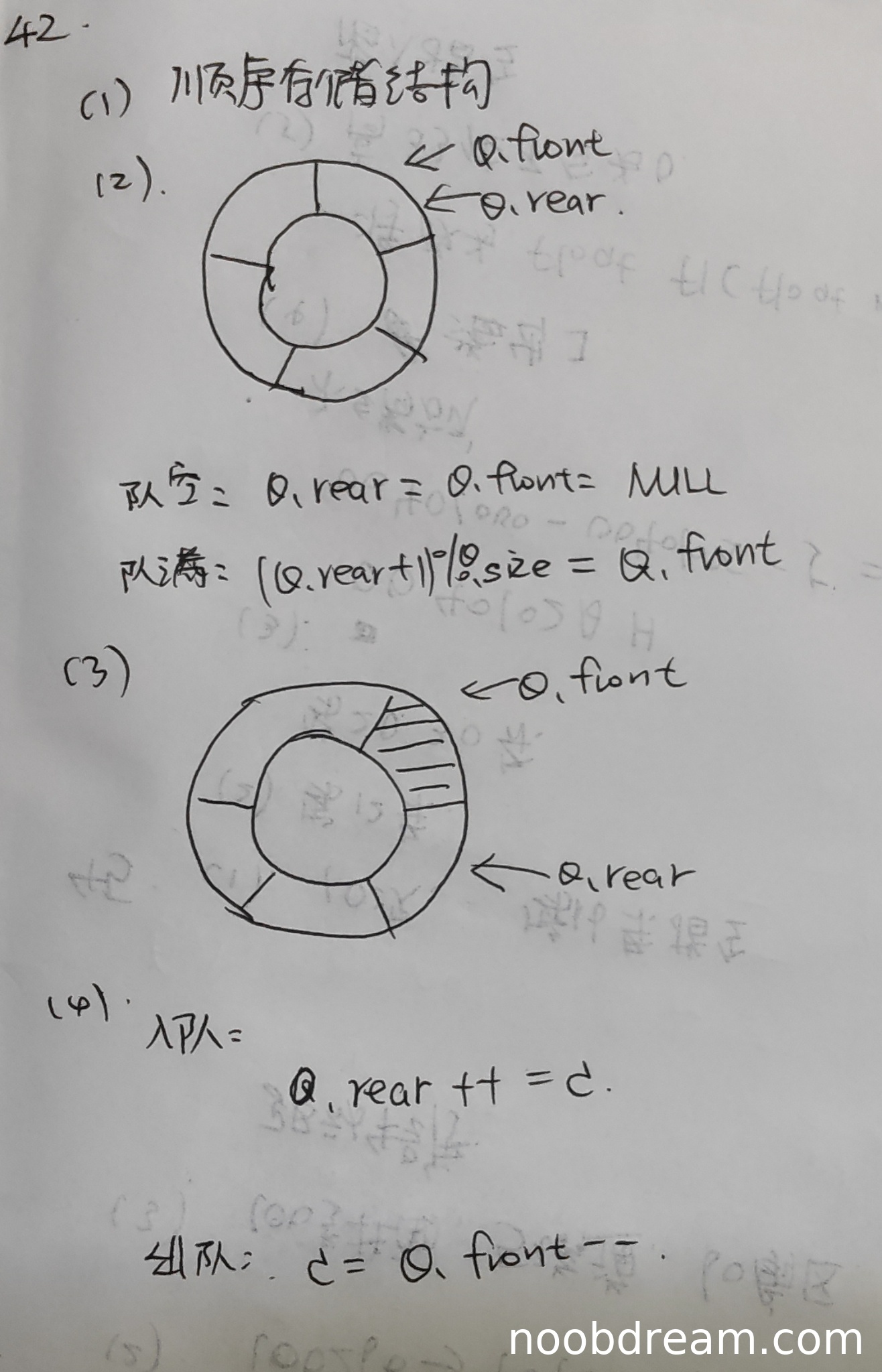
（1）得分及理由（满分2分）

学生答案选择“顺序存储结构”，标准答案为“链式存储结构”。题目要求“整个队列所占用的空间只增不减”，顺序存储结构在数组空间固定或成倍扩容时，难以满足“出队后空间可重复使用且只增不减”的要求（除非使用特殊设计的动态数组，但出队后空间通常不会释放，且扩容时复制元素时间复杂度不是O(1)）。学生选择顺序存储结构不符合题目设计意图，无法同时满足所有条件（尤其是空间只增不减且操作O(1)）。因此，本题得0分。

（2）得分及理由（满分4分）

学生给出了顺序存储结构下的队空和队满条件。队空条件为“Q.rear = Q.front = NULL”，这在顺序存储中通常不这样表示（顺序存储常用数组，front和rear是下标，初始为0或-1，NULL一般用于指针）。队满条件为“(Q.rear + 1) % size = Q.front”，这是循环队列的经典判断方法，但前提是数组大小固定。然而，题目要求“入队时允许增加队列占用空间”，即队列大小可变，这与固定size的循环队列矛盾。学生答案未体现空间动态增长且只增不减的特性，且初始状态描述不准确（未画出初始状态图）。因此，本部分答案不符合题目要求，得0分。

（3）得分及理由（满分2分）

学生未提供图示或文字描述第一个元素入队后的队列状态。根据作答内容，无法判断其状态。因此，本题得0分。

（4）得分及理由（满分2分）

学生给出的入队操作为“Q.rear++ = c”，出队操作为“c = Q.front--”。这是顺序存储（非循环）下的简单操作，但存在严重问题：
1. “Q.rear++ = c”在C语言中可理解为先赋值再后移，但未处理队满情况，且若为循环队列，rear移动需取模。
2. “c = Q.front--”是出队时front减减，这不符合队列先进先出的特性（通常出队是front加加或移动）。
3. 未体现空间动态增加和只增不减的要求，操作时间复杂度虽为O(1)，但整体设计不满足题目条件。
因此，本部分答案逻辑错误，得0分。

题目总分：0+0+0+0=0分