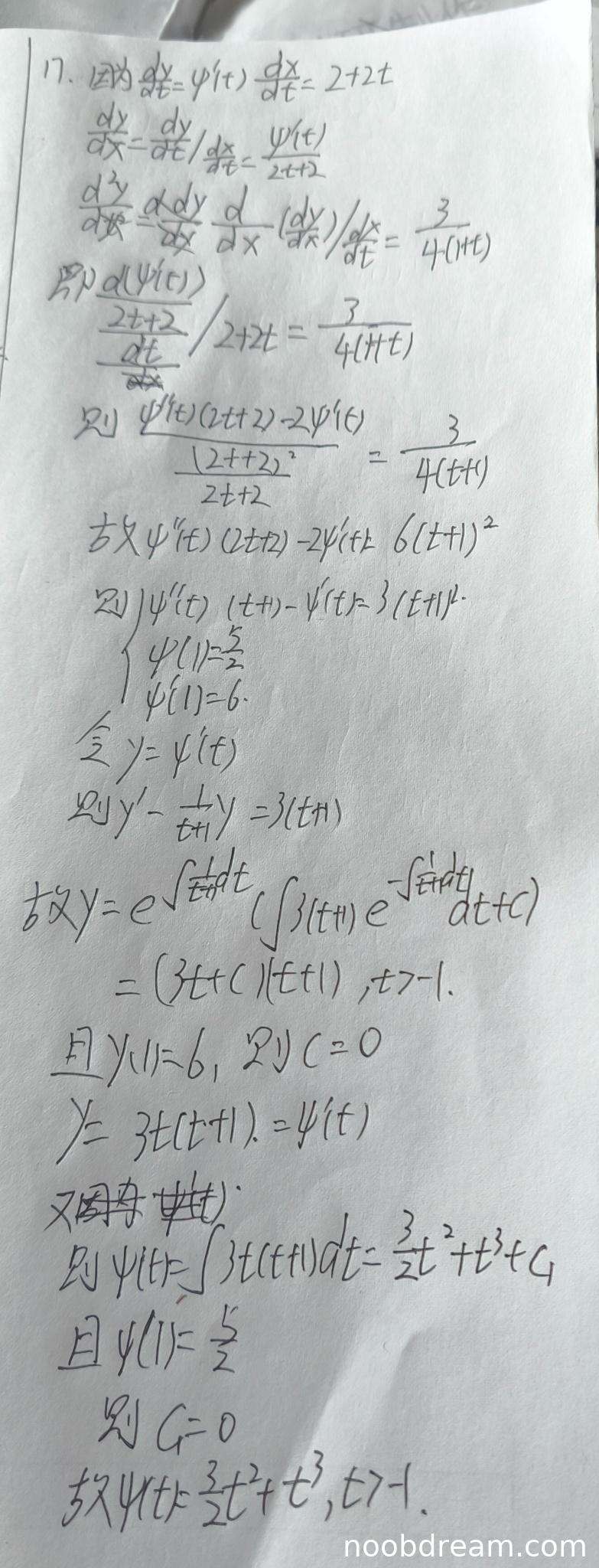
评分及理由

（1）得分及理由（满分10分）

本题满分10分。学生作答提供了两次识别结果，核心思路与标准答案完全一致：先由参数方程求导公式计算一阶和二阶导数，利用已知二阶导数建立关于 \(\psi(t)\) 的微分方程，然后通过一阶线性微分方程的解法求出 \(\psi'(t)\)，再积分并利用初始条件确定常数，最终得到 \(\psi(t)\)。

具体步骤中：
- 第一次识别结果在推导 \(\frac{d^{2}y}{dx^{2}}\) 时，表达式 \(\frac{\psi^{\prime}(t)(2t + 2)-2\psi^{\prime}(t)}{(2 + 2t)^{2}}\div\frac{2t + 2}{2t + 2}\) 书写略显混乱，但最终得到了正确方程 \(\psi^{\prime\prime}(t)(2t + 2)-2\psi^{\prime}(t)=6(t + 1)^{2}\)。
- 随后将方程化为 \(\psi^{\prime}(t)(t + 1)-\psi(t)=3(t + 1)^{2}\)，此处出现了明显的逻辑错误：左边第二项应为 \(\psi'(t)\) 而非 \(\psi(t)\)。这属于推导错误，应扣分。
- 但后续步骤中，学生“令 \(y = \psi^{\prime}(t)\)”后，写出的微分方程 \(y^{\prime}-\frac{1}{t + 1}y = 3(t + 1)\) 是正确的（尽管由错误的上一步直接得到此方程在逻辑上不连贯，但此方程本身正确）。
- 之后求解一阶线性方程、利用 \(\psi'(1)=6\) 确定常数、积分、再利用 \(\psi(1)=\frac{5}{2}\) 确定积分常数，这些步骤均正确，且最终答案 \(\psi(t)=\frac{3}{2}t^{2}+t^{3}\) 正确。

第二次识别结果在关键步骤上更清晰且正确：
- 推导 \(\frac{d^{2}y}{dx^{2}}\) 过程正确，得到 \(\psi^{\prime\prime}(t)(2 + 2t)-2\psi^{\prime}(t)=\frac{6(1 + t)^{2}}{2 + 2t}\)，化简后得到正确方程 \(\psi^{\prime\prime}(t)(1 + t)-\psi^{\prime}(t)=3...