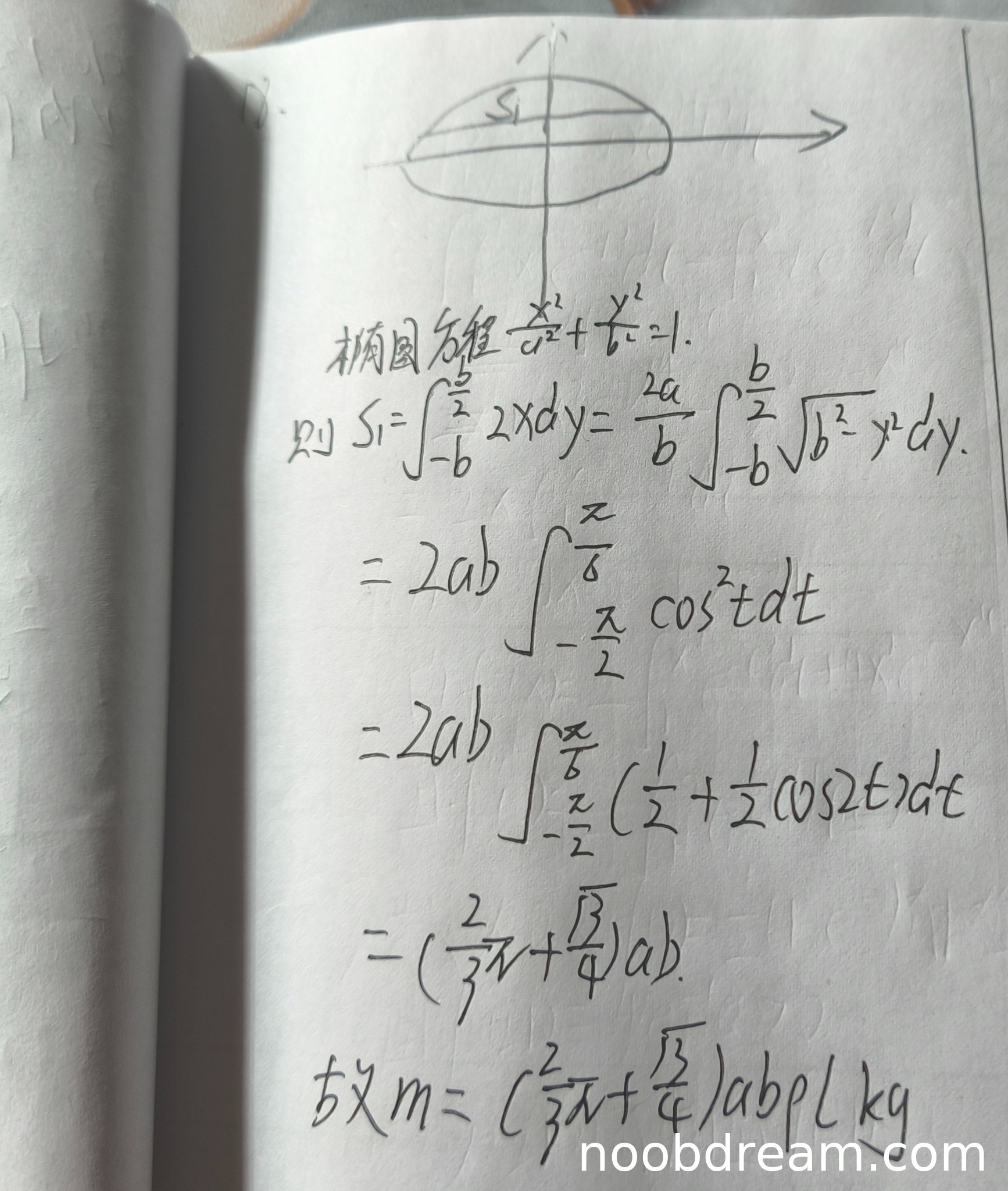
评分及理由

（1）得分及理由（满分10分）

本题满分为10分。学生作答分为两次识别结果，核心内容一致，仅在最终质量表达式上略有差异（第一次识别结果漏写了长度l）。

分析如下：

1. 思路与步骤：学生正确建立了坐标系，给出了底面椭圆方程，确定了积分上下限（从y=-b到y=b/2），并正确写出了油截面面积的积分表达式 \( S = \int_{-b}^{b/2} 2x \, dy \)。此部分思路完全正确，与标准答案一致。
2. 积分计算：学生正确进行了变量代换 \( y = b \sin t \)，并确定了对应的积分限 \( t \) 从 \( -\pi/2 \) 到 \( \pi/6 \)。积分过程 \( \int \cos^2 t \, dt \) 化为 \( \int (\frac{1}{2} + \frac{1}{2} \cos 2t) \, dt \) 并计算，最终得到面积 \( S = (\frac{2\pi}{3} + \frac{\sqrt{3}}{4}) ab \)。此计算过程与结果均正确。
3. 质量计算：
   • 第一次识别结果为 \( m = (\frac{2}{3}\pi+\frac{\sqrt{3}}{4})ab\rho \, \text{kg} \)，这里遗漏了柱体的高 \( l \)，属于逻辑错误（质量应为体积乘以密度，体积是截面积乘以长度l）。
   • 第二次识别结果为 \( m = (\frac{2}{3}\pi+\frac{\sqrt{3}}{4})ab\rho l \, \text{kg} \)，此表达式完全正确。
   根据题目要求“对学生作答进行了两次识别，只要其中有一次回答正确则不扣分”，且第二次识别结果正确，因此不因第一次识别结果中漏写 \( l \) 而扣分。
4. 其他：学生作答简洁，没有无关错误。最终答案与标准答案 \( m = (\frac{2\pi}{3}+\frac{\sqrt{3}}{4})abl\rho \) 完全一致（常数顺序不影响）。

综上，学生作答思路正确，计算准确，最终答案正确。根据评分要求，应给予满分。

得分：10分

题目总分：10分